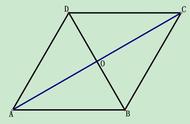
分析:求阴影部分的面积,阴影部分由三个三角形组成,如果一个一个求三角形的面积,比较繁琐,如果用平行四边形的中心对称性进行转化就可以轻松解决了。可以证明△BOF与△DOE全等,根据全等三角形的面积相等,可将△BOC的面积转化为△DOE的面积,那么阴影部分的面积即为△ACD的面积,而△ACD的面积又等于平行四边形ABCD 面积的一半。
解:∵四边形ABCD是平行四边形,
∴AD=CB,DC=BA.
∵AC=CA,
∴△ABC≌△CDA.
∴S△ABC=S△CDA=SABCD÷2=15(cm2).
∵四边形ABCD是平行四边形,
∴OD=OB,AD∥BC.
∴∠OED=∠OFB,∠EDO=∠FBO.
∴△DOE≌△BOF,
∴S△DOE=S△BOF.
∴S阴影部分=S△BOF+S△AOE+S△COD =S△DOE+S△AOE+S△COD=S△CDA=15 cm2.

巩固练习:如图,在ABCD中,对角线AC,BD交于点O,EF过点O与AB交于点E,与CD交于点F,GH过点O与AD交于点G,与CB交于点H。求证:GF=EH.

构造法是根据题设条件或结论具有的特征、性质,构造出满足条件或结论的数学模型,借助该数学模型来解决原数学问题的解题方法.对于某些问题,常采用构造平行四边形的方法,从而利用平行四边形的性质使问题变得简单。

分析:本题可以利用倍长中线法来解题。延长AD至N,使DN=AD,连接BN,可证明△BDN≌△CDA(SAS),则BN=AC,∠CAD=∠N,根据AE=EF,得∠CAD=∠AFE,可证出∠N=∠BFG,即得出AC=BF,也可构造平行四边形来解决。
证明:如图,延长AD至N,使DN=AD,连结BN,CN,则四边形ABNC是平行四边形.