在平行四边形这一章节中,除了几何思想外,还可以与代数思想相结合在,真正做到数形结合。平行四边形中方程思想、转化思想与构造思想很重要,需要做到活学活用。

在几何图形中,有些题目需要设未知数找等量关系比直接解题要方便简单,常见的为已知四边形的面积、周长、线段的和差关系等。
例题1:如图,四边形ABCD是平行四边形,AE⊥BC于E,AF⊥CD于F,AE=4,A=5,四边形ABCD的周长为36,求AB,BC的长.

分析:已知平行四边形的周长,利用公式可知邻边之和为周长的一半,根据平行四边形的面积不变(即等积法)可得到邻边之间的倍数关系,通过设两个未知数,得到关于邻边的方程组,求出方程组的解即可。
解:在ABCD中,CD=AB.
∵ABCD的面积=BC·AE=CD·AF,
AE=4,AF=5,
∴4BC=5CD,即BC:CD=5:4
设BC=5x,CD=4x,
又2(AB+BC)=36,
∴AB+BC=18,即BC+CD=18,
∴5x 4x=18,解得:x=2
∴BC=5x=10,CD=4x=8,
即AB=8,BC=10.

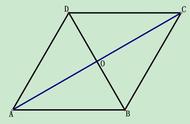
巩固练习:已知平行四边形ABCD的周长为28,对角线AC,BD相交于一点O,且△AOB的周长比△BOC的周长大4,求AB,BC的长.
转化思想平行四边形的一条对角线可将平行四边形分割成两个全等的三角形,两条对角线可将平行四边形分割成四个三角形,相对的两个三角形全等,四个三角形的面积相等,都等于整个平行四边形面积的四分之一。解决四边形的长度、面积问题时有些时候需要转化为三角形问题,有时也需要用四边形的中心对称性进行转化。
例题2:如图,在ABCD中,对角线AC,BD相交于点O,过点O作直线交AD于点E,交BC于点F,若ABCD的面积为30 cm2,求图中阴影部分的面积.