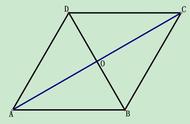
力的合成并不是指物体所受到的几个力硬生生的合在一起,而是指将物体受到的几个力等效的合在一个作用点上,其合在物体上的共作用点只有一个,而且都在物体所受到的力方向的延长线上或同一个水平面上。这种力学中常见的受力分析,不仅简化了从事物理研究工作者的体力劳动,而且还能直观的将物体的受力情况清晰的表达出来。

力的合成不是简单的加法运算,而是一种复杂的几何运算。对于在同一条直线上的力,其合力可以用加法进行直接运算。这时,我们只需选择其中一个力的方向为正方向,与这个力方向相反的取负,与这个力方向相同的取正,然后带入公式中就可以求出此水平面上的物体受力大小。

如果求出这个物体的受力大小为负数,说明物体受到的力与原来选取正方向的力方向相反,如果求出物体的受力大小为正数,则说明此时物体的受力情况与原来选取的力的方向一直。故而,在物体受力分析中,是没有硬性规定假设物体受到哪个力为正方向的。

为了进一步了解物体等效合力的相关常识,我们可以选择一条橡皮筋,然后将橡皮筋的一端固定在墙面上,将橡皮筋的另一端系上一个质量很轻的物体,在物体的另一端系上绳子。此时,我们水平用力拉绳子(此时的力可以记作为F)使橡皮筋伸长一定的距离,并记录下此距离的长度为d。
然后我们撤下这跟绳子,在物体的上下边分别系上绳子,然后同时拉这两根绳子,其受到的力为F1和F2,使橡皮筋的移动距离为d。此时,物体受到的这两个力F1与F2可以等效为F,也就是说,力F就是F1与F2的合力了。这就是物体合力的等效作用。