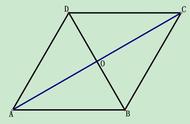
而力F并不是简单的F1与F2的加法运算,这里面就涉及到了数学函数问题。在运用数学函数解决物体受力大小的情况下,就不得不提出一个“平行四边形”法则了。在力的合成过程中,是逐次进行合成的,从两个力合成完后,其合力与物体的受到的第三个力进行合成,直到合成至物体受到的第N个力。

物体的合力并不是物体真实受到的力,而是为了方便计算与分析。其等效合力的方向,总是在两个分力所组成的平行四边形的中心线上,如果达不到这个要求,那么这两个力就不能进行合成,当然,直线上的力的合成是一个特殊情况。
在这种情况下,平行四边形就无形的被分成了两个三角形了,运用数学相关的三角函数知识,只要知道其中一个力的大小以及一个角度,就可以求出其它力的大小。例如,在一块倾斜角度为a的木板上放置着一个静止的物体。

此时的物体受到了竖直向下的重力G,垂直与木板向上的支持力F1,以及沿着木板向上的静摩擦力f。由于物体处于静止状态,要想其中的一个力与静摩擦力f平衡,就必须得把重力进行分解。
其中,重力的一个分力F2沿着木板向下,这个分力F2与静摩擦力方向相反,大小相等。如果F2与静摩擦f的大小不相等,则物体就会向下滑落。还有,重力的另外一个分力F3垂直于木板向下,此时F3与木板对物体的支持力同样平衡了。所以,物体才能在木板上处于静止状态。

由于我们知道了物体的重力为G,倾斜的木板角度为a。通过三角形的相似原理与三角函数关系式就可以求出物体此时受到的静摩擦力。故而,静摩擦力f就等于重力G乘以sina,其表达式为f=Gsina。
从力的合成中求力的大小中可以看出,物理与数学是分不开的,一个伟大的物理学家同时也是一个伟大的数学家。力的合成与分解在宏观的物理界中是运用得最多的,这其中最著名的人物就是牛顿了。