例题:已知x、y均为有理数,且x^2 2y √2y=17-4√2,则x y的值为几?
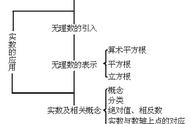
这道题是一个方程两个未知数x、y,用常规方法肯定无法求出x和y的值,解决此题肯定有自己的门道。已知中专门告诉x和y为有理数,而方程中又出现无理数√2,就意味着需要运用实数的性质来解决。
首先回顾实数的性质:
乘法:有理数×有理数=有理数,有理数(0除外)×无理数=无理数,无理数×无理数=有(无)理数;
加法:有理数 有理数=有理数,有理数 无理数=无理数。上面这道题通过移项后明显是有理数 无理数=0(有理数),那么说明无理数√2(y 4)只有等于0才能满足条件,即就是y 4=0,求出y=负4。

例题图
解答过程:
移项得:x^2 2y-17 √2y 4√2=0
合并:x^2 2y-17 √2(y 4)=0
由法则可知:√2(y 4)=0
解得:y=-4
代入:x^2 2y-17=0
解得:x=正负5
所以x y=1或负9。
后记:回顾这道题的解答过程,掌握实数性质是关键,更要善于发现解决问题的突破口就是其中两点,有理数和√2,如果没有这种数学灵感,光靠背记性质也是没有用的。
,