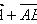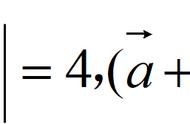第二章 平面向量
2.1 平面向量的实际背景及基本概念
2.1.1 向量的物理背景与概念
(1)向量的概念
①向量的判定
②向量的性质
2.1.2 向量的几何表示
(1)向量的表示方法
①向量的模
②向量的几何意义及其应用
③向量的几何表示
(2)单位向量与零向量
①零向量的性质
②单位向量的性质
③零向量与单位向量的综合判定
2.1.3 相等向量与共线向量
(1)相等向量与共线向量
①相等向量与共线向量的性质和判定
②各类向量特征的综合判定
③相等向量与共线向量的应用
④几何图形中的相等向量与共线向量
2.2 平面向量的线性运算
2.2.1 向量加法运算及其几何意义
(1)向量加法运算及其几何意义
①求作和向量
②向量加法的三角形不等式
(2)向量加法的定义及其几何意义的应用
①利用向量的加法求位移
②向量的加法在运动学中的应用
③向量的加法在物理学中的应用
④向量加法在平面几何中的应用
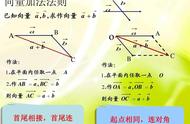
(3)向量加法的平行四边形法则
①向量加法的平行四边形法则
②利用向量的加法求模长
③判定四边形的形状
(4)向量的加法运算与运算规律
①化简向量
②证明几何图形中的向量等式
③几何图形中的向量加法运算
2.2.2 向量减法运算及其几何意义
(1)向量减法运算及其应用
①向量减法运算及其几何意义
②求作差向量
③向量减法的三角形不等式
(2)向量加法、减法的几何意义的应用
①向量、和向量与差向量的模之间的特殊关系
(3)向量加减法的综合运算及应用
①利用向量的加、减法化简向量
②几何图形中向量的加、加法运算
③用已知向量表示未知向量
④利用向量的加、减法运算求向量的模
2.2.3 向量数乘运算及其几何意义
(1)向量数乘的定义及运算
①向量数乘的定义及几何意义
②向量数乘运算及运算律
③利用向量的数乘运算求数乘系数
(2)向量的线性运算及应用
①向量的线性运算
②用已知向量表示未知向量
③向量线性运算的应用
(3)向量共线定理及其应用
①利用向量共线定理判定向量共线
②利用向量共线定理判定三点共线
③利用向量共线定理求参数
④用已知向量表示未知向量
⑤向量共线定理在平面几何中的应用
⑥三点共线定理的应用
2.3 平面向量的基本定理及坐标表示
2.3.1 平面向量基本定理
(1)平面向量基本定理
①基底的含义与性质
②基底的判定
③用基底表示向量
(2)平面向量的夹角求向量的夹角
①求向量的夹角
(3)平面向量基本定理的应用
①利用平面向量基本定理求线段的长度比
②利用平面向量基本定理求参数
2.3.2 平面向量的正交分解及坐标表示
(1)平面向量的正交分解及坐标表示
①平面向量的正交分解及坐标表示
②利用平面向量的正交分解求向量的坐标
2.3.3 平面向量的坐标运算
(1)平面向量的坐标运算
①平面向量的坐标运算
(2)平面向量的坐标运算的应用
①利用平面向量的坐标运算求点的坐标
②利用平面向量的坐标运算求向量的坐标
③利用平面向量的坐标运算求参数
④利用平面向量的坐标运算求轨迹方程
⑤用坐标形式下的基底表示向量
2.3.4 平面向量共线的坐标表示
(1)平面向量共线的坐标表示
①向量共线的判定与证明
②三点共线的判定与证明
(2)向量共线的坐标表示的应用
①已知三点共线求点的坐标
②已知向量共线求向量的坐标
③已知向量共线求参数
④利用三点共线求参数
2.4 平面向量的数量积
2.4.1 平面向量数量积的物理背景及其含义
(1)平面向量数量积的概念与几何意义
①平面向量数量积的概念与几何意义
(2)平面向量的投影
①求向量的投影
(3)平面向量数量积的运算性质与法则
①向量的运算性质与法则
②求向量的数量积的最值
(4)平面向量数量积的应用
①利用数量积求向量的模
②利用数量积求向量的夹角
③已知向量夹角求参数
④数量积在三角形中的应用
⑤向量模与夹角的综合应用
2.4.2 平面向量数量积的坐标表示、模、夹角
(1)平面向量数量积的坐标表示与应用
①坐标形势下的数量积运算
②已知数量积求参数
③已知数量积求向量的坐标
(2)向量平行与垂直的坐标表示的应用
①已知向量平行求参数
②已知向量垂直求参数
③向量垂直的坐标表示的综合应用
④向量平行与垂直的坐标表示的综合应用
(3)平面向量夹角的坐标表示与应用
①求坐标形式下的向量夹角
②已知坐标形式下的向量夹角求参数
③平面向量模与夹角的坐标表示的综合应用
(4)平面向量模与夹角的坐标表示的应用
①利用坐标求向量的模
②平面向量模的坐标表示的应用
(5)平面向量投影的坐标表示与应用
①利用坐标求向量的投影
2.5 平面向量应用举例
2.5.1 平面几何中的向量方法
(1)平面几何中的向量法
①判定多边形的形状
②向量与直线方程
③向量与轨迹方程
④利用向量解决平面几何问题
2.5.2 向量在物理中的应用举例
(1)向量在力学中的应用
①求合力
②求分力
③求做功
④求夹角
(2)向量在运动学中的应用
①求速度
②求位移
③求方向
④求时间
章末复习课
(1)数形结合思想在向量问题中的应用
①数形结合思想在向量问题中的应用
(2)基底思想在解题中的应用
①基底思想在解题中的应用
(3)向量坐标在解题中的应用
①向量坐标在解题中的应用
,