一、向量的有关概念
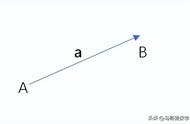
(一)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或模).数量只有大小没有方向。
(二)零向量:长度为0的向量,其方向是任意的.记作0.
(三)单位向量:长度等于1个单位的向量.单位向量的方向不确定,且有无数个。
(四)平行向量(共线向量):方向相同或相反的非零向量.记作a∥b.
规定:0与任一向量平行.
(五)相等向量:长度相等且方向相同的向量.记作a=b.
(六)相反向量:长度相等且方向相反的向量.a b=0.
二、向量的线性运算
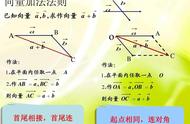
(一)加法,求两个向量和的运算,可利用三角形法则和平行四边形法则运算。
运算律:
(1)交换律:a+b=b+a.
(2)结合律:(a+b)+c=a+(b+c)
(二)减法,减去一个向量相当于加上这个向量的相反向量.
运算律:a-b=a+(-b)
(三)数乘,求实数λ与向量a的积的运算.
(1)|λa|=|λ||a|;
(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;
当λ=0时,λa=0.
运算律:
λ(μa)=λμa;
(λ+μ)a=λa+μa;
λ(a+b)=λa+λb.

三、向量共线定理
量a(a≠0)与b共线的充要条件是存在唯一一个实数λ,使得b=λa.
1.平面向量的基本定理
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
其中,不共线的向量e1,e2叫做表示这一平面内所有向量的一组基底.
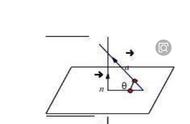
2.平面向量的正交分解
把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.
3.平面向量的坐标运算
(1)向量加法、减法、数乘运算及向量的模
设a=(x₁,y₁),b=(x₂,y₂),则
a+b=(x₁+x₂,y₁+y₂),a-b=(x₁-x₂,y₁-y₂),λa=(λx₁,λy₁),
|a|==.
(2)向量坐标的求法
①若向量的起点是坐标原点,则终点坐标即为向量的坐标.
②设A(x₁,y₁),B(x₂,y₂),则AB=(x₂-x₁,y₂-y₁),
∣AB∣=
4.平面向量共线的坐标表示
设a=(x₁,y₁),b=(x₂,y₂),则a∥b⇔x₁y₂-x₂y₁=0.
四、平面向量数量积的有关概念
1.有关概念
(1)向量的夹角:已知两个非零向量a和b,记OA=a,OB=b,则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角.
(2)数量积的定义:已知两个非零向量a与b,它们的夹角为θ,则a与b的数量积(或内积)a·b=|a||b|cosθ.
规定:零向量与任一向量的数量积为0,即0·a=0.
(3)数量积的几何意义:数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积.
2.平面向量数量积的性质及其坐标表示
设向量a=(x₁,y₁),b=(x₂,y₂),θ为向量a,b的夹角.
(1)数量积:a·b=|a||b|cosθ=x₁x₂ y₁y₂.
(2)模:∣a∣==.
(3)夹角:cosθ=。
(4)两非零向量a⊥b的充要条件:a·b=0x₁x₂ y₁y₂=0.
(5)∣a·b∣≤∣a∣∣b∣(当且仅当a∥b时等号成立)∣xx yy∣≤.
3.正余弦定理