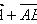1、向量的定义:既有大小又有方向的量叫做向量。
(向量两大要素:大小和方向,二者缺一不可。向量的大小是代数特征,方向是几何特征。)
2、向量的表示:
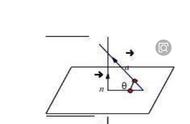
向量可以用有向线段(带有方向的线段)表示,有向线段的长度表示向量的大小,线段的箭头指向就是向量的方向,线段的起点叫做向量的起点,线段的终点叫做向量的终点。
一般地,可以用有向线段的两个端点(并且在端点上加上“→”符号)来表示,也可以用加租的小写字母来表示。
例如:下图中向量表示为AB向量(无法在AB上添加箭头,抱歉!)(读作AB向量)或“a“(读作a向量,书写时应在字母上加“→”符号)

3、向量的模(长度):
(1)向量模的概念:表示向量的有向线段的长叫做向量的模,也叫做向量的长度,如上图中,a向量记作|a|。
(2)平行向量的概念:方向相同或相反的非零向量,也叫做共线向量,用符号“∥”表示。
(3)零向量的概念:模为零的向量叫做零向量,记作“0”,零向量的方向是不确定的,零向量与任一向量平行。
(4)相等向量的概念:如果两个向量的模相等且方向相同,那么这两个向量相等,即:互为相等向量。
(5)相反向量的概念:如果两个非零向量的模相等且方向相反,那么这两个向量互为相反向量(负向量)。
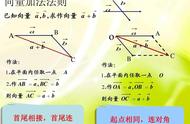
二、向量运算法则1、向量的加法:
①三角形法则:
已知非零向量a,b(已知向量的方向和大小),在平面上任取一点A,作(AB向量) =a,(BC向量)=b,并且作(AC向量) ,则(AC向量) 叫做向量a与向量b的和,记作a b。
如图所示:(AC向量)= a b

②平行四边形法则:
已知非零向量a,b(已知向量的方向和大小),在平面上任取一点A,作(AB向量)=a,(AD向量)=b,以AB,AD为邻边作平行四边形ABCD,则(AC向量)= a b。
如图所示:(AC向量)= a b

③运算律:
加法交换律:a b=b a
加法结合律:(a b) c=a (b c)
2、向量的减法:
已知非零向量a,b(已知向量的方向和大小),在平面上任取一点O,作(OA向量) =a,(OB向量)=b,作(BA向量),则(BA向量)=a-b。
一个向量减去另一个向量等于加上它的相反向量,即:a-b=a -(b)。
如图所示:(BA向量)=a-b