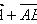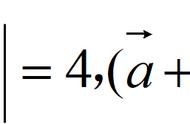一、向量加减法运算的基本方法
(1)利用相反向量统一成加法(相当于向量求和);
(2)运用减法公式向量AB﹣向量AC=向量CB (正用或逆用均可);
(3)运用辅助点法,利用向量的定义将所有向量转化为以一确定点为起点的向量,使问题转化为有共同起点的向量问题。




二、用已知向量表示未知向量的思路方法
解决这类问题时,要根据图形的几何性质,正确运用向量的加法、减法以及共线(相等)向量,要注意向量的方向及运算式中向量之间的关系。当运用三角形法则时,要注意两个向量起点的位置,当两个向量共起点时,可以考虑向量的减法。
常用结论:任意一个非零向量一定可以表示为两个不共线向量的和(差),即向量AM=向量AB 向量BM以及向量AB=向量NB-向量NA (M ,N均是与向量AB在同一平面内的任意点)。

三、向量的模的求法
向量a 向量b,向量a-向量 b的几何意义是以向量a ,向量b为邻边的平行四边形的对角线表示的有向线段,故求解它们的模时,注意结合它们所在的平行四边形去求解。
四、求解向量加減减法实际应用题的步骤
(1)表示:用向量表示实际问题中既有大小又有方向的量;
(2)运算:利用向量加减法的运算法则进行向的运算,并利用直角三角形等知识求出有关线段的长和夹角;
(3)作答:根据題意作答。
,