四点共圆的几种判断方法
若在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
四点共圆的判断方法较多,下面分述及证明如下。
一、若四个点到一个定点的距离相等,则这四个点共圆
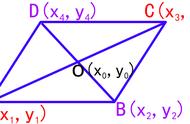
如下图,OA=OB=OC=OD,作以O点为圆心,OA为半径的圆,则A、B、C、D四点均在圆上,即四点共圆。
从圆的基本概念可以很好理解:圆是平面上的一种几何图形,指的是到一个定点距离为定值的所有点的集合,这个定点为圆心,定值的距离为圆的半径。

二、同(共)斜边的直角三角形的顶点共圆
如下图,四边形ABCD中,∠A=∠C=90°,则A、B、C、D四点共圆。

证明:设斜边DB的中点为O,根据直角三角形斜边的中线等于斜边的一半得知,OA=OB=OC=OD,故则A、B、C、D四点共圆,BD为圆的直径,圆心为O。
三、若一个四边形的一组对角互补,则这个四边形的四个点共圆。
如下图,四边形ABCD中,∠A ∠C=180°。求证:A、B、C、D四点共圆。

证明:本题证明采用反证法:已知四边形ABCD中,∠A ∠C=180°,所以∠D ∠B=180°,∠ADC =180°-∠B。
过A、B、C三点作圆O,则D点要么在圆内,要么在圆外,如果这两种情况都不可能,那么点D只能在圆上。
先假设点D在圆内,延长AD交圆于D′,连接CD′,则∠D′=180°-∠B,故∠ADC =∠D′,这与“三角形外角大于不相邻的内角”定理相矛盾,故点D不在圆内。
再假设点D在圆外,同样可证明点D不在圆外。
最后只有一种情况就是点D在圆上,即A、B、C、D四点共圆。
四、 若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆。
该结论基于“若一个四边形的一组对角互补,则这个四边形的四个点共圆”很容易证明,在此不再赘述。
五、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆。亦可描述为:两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,那么这两个三角形有公共的外接圆。
证明:如下图,先作△ABC的外接圆O,在圆O劣弧AB上取点E,E、C两点位于AB的异侧。
这样A、C、B、E四点共圆,∠C ∠E=180°。
已知∠C=∠D,故∠D ∠E=180°。
由此A、E、B、D四点共圆。
因为过不共线的三个点(A、B、E)可以作一个圆且只可以作一个圆O,所以A、B、C、D四点共圆,也就是说三角形ABC和三角形ABD有公共的外接圆。