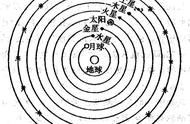
我们看爱因斯坦是怎么推广相对论的。
引力质量与惯性质量等价;
参照框架的相对加速度等价于一个均匀引力场。
据说有这么两件事情,其实就是研究一个小物体被大物体吸引的牛顿力学方程。爱因斯坦做的第一件事,就是是认定引力质量和惯性质量等价,惯性质量和惯性质量可以约掉,就是这么简单。
方程左边是加速度,右边是引力势。如果加速度是相对于一个匀加速的参照系,左边就得加个常数加速度,另一边也得加上同样的项,而这个常数就是恒定、均衡的,空间均匀的引力场,参照框架的相对加速度,等价于一个均匀的引力场,这个引力场和加速度凑到一起了。
爱因斯坦说出事了,因为你回顾一下牛顿三定律,第一句话说的是什么?说的是外力等于零的情况下,这个运动是惯性的,可是现在我的加速度和引力分不开了,什么叫加速度等于零的匀速直线运动?爱因斯坦觉得必须把惯性运动这个概念给修正。所以在广义相对论里面,惯性的定义变成了除了引力之外的其他力等于零的情况下的运动叫惯性运动,也就是说从高空往下落的过程中这是惯性运动。
当然做这样的惯性运动也叫自由落体,大家知道自由的下落,说自由下落这个过程是非常 happy 的过程,一个人从高空坠落这个过程是非常 happy 的,什么时候让你感觉到你不 happy 呢,是大地接着你,不让你堕落的时候,痛苦才来的。
据说爱因斯坦 1913 年某一天下午才想明白,原来自由下落的过程是非常 happy 的过程,是感觉不到引力的过程,这个过程是可以当做惯性的,也就是说我可以把惯性运动的概念修订为:
除了引力之外的所有力为零下的运动状态叫惯性。

有了这些认识,原来是说要描述引力的,描述弯曲空间的事情变成如何描述加速度了。怎么描述加速度?我们回忆一下中学物理。有一个简单的例子,匀加速运动。大家想象一下,一辆车从你家地里开过之后,警察来了能看到什么?看到车轱辘印子,好的警察就要通过车轱辘印子判断你这个车是怎么开的。所以说人家很早就有这个思想,一个几何体和一个轨迹都要从他自身去找到描述,不能从外在的世界找到描述。我们知道圆是一维闭合的几何体,我们相当多的同学还有一个特别错误的概念,以为圆有圆心。我再提醒大家一下,圆没有圆心,圆心是引入的辅助的概念。
工人在一个地方要画个圆圈的时候,或者开车的时候画圆圈的时候,只要方向盘打个不变的角度,车会自动画出来圆圈,没有圆心,这是人家西方几何里早就有的思想。有了这些思想你再学人家相对论怎么描述的时候,突然就明白了。
比如说我们学的加速度都是位置对时间的二阶微分,如果回顾描述一条弯曲曲线会用到哪些几何的时候,你会发现人家都是描述位置对距离的二阶微分。
而这样一个知识其实在我们的日常生活里都是这样的。比如你如果描述从北京到上海的 G3、G4 高速是怎么描述的?不是给出坐标相对时间的变化,而从来都是车所在的位置相对于起点多少公里处,你告诉我顺着这条路多少公里处就行了,我就能找到你了。所以描述一条曲线正确的参数是这条曲线的长,这样的好处是如果位置相对于轨迹弧长变化的话,你的加速度和弧长本身是垂直的,永远是向心加速度,或者匀速圆周运动告诉我们,加速度和曲率成反比。如果你用这样一个二阶微分公式来写加速度的话,加速度本身就等于轨迹那一点的曲率。于是乎描述加速度这件事情又变成描述曲线怎么弯曲的了,我们需要学的是描述轨迹或者存在的曲面,或者那个空间是怎么弯曲的学问了。
描述曲线怎么弯曲运动以及描述曲面怎么弯曲,这样的一个几何学问又是来自于我们日常生活,尤其是像法国和德国这种地方,生活在丘陵地带的地方,他们的科学家很早做大地测量的时候就知道大地是弯的,怎么在地图里把弯的事情都给表达清楚,就是他们在实践中所创造的学问。据说那个数学大神,被称为数学第一人的高斯,就是一直在忙着测德国地形如何弯曲的过程中发展出了测地线这个学问,在这个过程中接到了他家里派人,匆匆忙忙赶到工作地点送信的,说您赶紧回家吧,您夫人不行了。高斯竟然说,再等一会儿,我马上就完。
在这样一个过程中,高斯、黎曼他们完成了对弯曲空间如何描述的这样一门学问,当然这门学问如何描述弯曲,还有牛顿,以及还有一个法国 16 岁的少年克莱洛,写出了二维平面曲线和三维空间曲线。
1729 年克莱洛写出这样公式的时候仅仅 16 岁,但是在论文后面写出了一个要求,我要当院士。16 岁是未成年人,不能让他当院士,所以就被拒绝了。两年以后,他又写出了三维空间曲线曲率的表达式,就是我们学经典力学里面三维空间标架,切线、法线和第二个法线标架,就是克莱洛 18 岁的时候给我们引进的,他在论文后面又写出这样的要求,我要当院士。大家实在是没脸再拒绝他了,所以克莱洛 18 岁当上的院士。
这些曲率的公式就不给大家讲了,但是越弯曲意味着蓄的能量越大,这一点我们的老祖宗早就告诉我们了,那就是弓。弓拉得越弯力越大,曲率和能量密度的关系我们应该是知道的。爱因斯坦他们后来得到相对论场方程更多借助于材料科学和结构力学方面的知识,就不跟大家讲细节了。
现在我们知道,我们描述时空弯曲就是描述加速度,描述引力也是描述加速度。加速度、引力、曲率、弯曲时空,这些东西凑到一起了,现在我们只需要学会给定弯曲时空,我们知道弯曲时空两点之间距离,就能求出它的曲率,这是爱因斯坦要学的学问。

这一套学问爱因斯坦会不会呢?爱因斯坦不会,这也正常,谁的学问都是从不会到会慢慢学的。但是爱因斯坦不一样,爱因斯坦是贵人,有人相助,谁呢?爱因斯坦的大学同学马塞尔·格罗斯曼(Marcel Grossmann),给爱因斯坦安排了在专利局的工作,思考火车、钟表和电报,于是有了狭义相对论。
爱因斯坦从 1907 年差不多干到 1912 年、1913 年,有很多种方案,最后都不行。到这个时候才明白了
要描述引力,需要有能够描述弯曲、加速度、曲率、弯曲时空的曲率的数学。
于是爱因斯坦问格罗斯曼有没有这方面的数学研究,格罗斯曼在图书馆给他查了一天告诉他,有!现在经过慕尼黑大学往南传到了意大利北面,形成学派,还出了一本书——《绝对微分》(absolute differential calculus),相对论其实就是研究绝对性,这个地方是绝对微分,现在我们叫张量分析。1907 年图利奥·列维-齐维塔(Tullio Levi-Civita)就开始研究相对论。
格罗斯曼告诉爱因斯坦有张量分析和这一本书以后,于是爱因斯坦就开始学习,这是爱因斯坦为了构造他的广义相对论,跟着张量分析这本书现学的。到 1915 年初的时候格罗斯曼介绍了列维-齐维塔跟爱因斯坦认识。一个数学家发现他的工作竟然有人感兴趣!所以你能想象到他的热情——列维-齐维塔这个意大利人用德文和法文一点一点写信教爱因斯坦。而在这冥冥之中,还有一点“宿命”的东西。爱因斯坦上初中的时候,他的爸爸妈妈跑到意大利北部城市米兰开电机厂,所以爱因斯坦说我小时候在意大利待过,请你用意大利语教我。
你们注意到一个问题没有?一个意大利人在用德语和法语,不厌其烦地教爱因斯坦。
弯曲空间的几何
爱因斯坦 1915 年上半年就掌握了张量分析,广义相对论就在这一页,特别简单,上图中第一个公式 就是两点之间的距离公式。虽然看起来特吓人,但其实在二维平面里就是勾股定理,没有什么其他的东西。如果我们初中老师愿意给我们往前稍微引申一点,那时候你学不懂,至少你知道的话,将来学广义相对论就不会害怕。
描述两点之间距离 的矩阵,对它进行微分就得到了这个联络
再进行微分,就得到了黎曼张量
这两个指标一收缩就是里奇张量 ,就是做两步微分的东西。
在上述两次微分的过程中,第一次微分得出了 Christoffel 符号,以此为几何的出发点,于是乎有了规范场论。给定一个联络,更加扩展地定义微分几何,这就是杨振宁先生工作的方向,也是华人数学家陈省身先生工作的方向。黎曼张量里这个黎曼也有来头。黎曼在他 1854 年的论文不仅确定了数学的内容,还是第一个使用了量子,并且也是指明了量子力学本质是几何量子化的一篇论文。
里奇张量则是描述时空怎么弯曲的,在意大利语里奇其名竟然就是弯曲的意思。