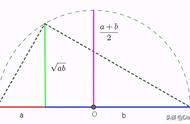
接下来我们来讨论一下这四个平均数的大小关系。
n个正数的平均数证明起来比较复杂,我们简化为讨论两个正数。
对于正数a、b:
A=(a b)/2
G=√(ab)
H=2/(1/a 1/b)
R=√[(a^2 b^2)/2]

我们首先讨论算术平均数与几何平均数的大小关系。
(√a-√b)^2
=(√a)^2-2√a√b (√b)^2
=a-2√(ab) b≥0
a b≥2√(ab)
(a b)/2≥√(ab)
A≥G
进一步
√(ab)≤(a b)/2
ab≤[(a b)/2]^2
由(√a-√b)^2=0,可得
a=b
这就是非常重要的均值不等式。
若a>0,b>0,则
①a b≥2√(ab)
②ab≤[(a b)/2]^2
当且仅当a=b时,不等式取等号。
①当ab为定值S时,a b的最小值为2√(ab)=2√S;
②当a b为定值P时,ab的最大值为[(a b)/2]^2=(P/2)^2=P^2/4;
口诀:积定和小,和定积大

接下来我们来讨论算术平均数与平方平均数的大小关系。
(a-b)^2=a^2-2ab b^2≥0
a^2 b^2≥2ab
2(a^2 b^2)
=(a^2 b^2) (a^2 b^2)
≥(a^2 b^2) 2ab=(a b)^2
a^2 b^2≥(a b)^2/2
(a^2 b^2)/2≥(a b)^2/4
=[(a b)/2]^2
√[(a^2 b^2)/2]≥(a b)/2
R≥A
最后我们来讨论几何平均数与调和平均数的大小关系。
2/(1/a 1/b)=2ab/(a b)
a b≥2√(ab)
1/(a b)≤1/2√(ab)
2/(1/a 1/b)=2ab/(a b)
≤2ab/2√(ab)=ab/√(ab)=√(ab)
2/(1/a 1/b)≤√(ab)
H≤G
把以上结论连列起来:
2/(1/a 1/b)≤√(ab)
≤(a b)/2≤√(a^2 b^2)/2
我们举个简单的例子验证一下这个结论。
令a=2>0,b=3>0
H=2/(1/2 1/3)=12/5=2.4
G=√(2×3)=√6≈2.45
A=(2 3)/2=5/2=2.5
R=√[(2^2 3^2)/2]=√6.5≈2.55
H≤G≤A≤R

以上结论都可以从两个正数推广到n个正数,由于证明比较复杂,这里不作详细证明,大家只需要记住结论即可。
n/(1/a1 1/a2 … 1/an)
≤(n)√(a1a2…an)
≤(a1 a2 … an)/n
≤√[(a1^2 a2^2 … an^2)/n]
调和平均数≤几何平均数
≤算术平均数≤平方平均数
,