【动量定理与动能定理】动量定理中的平均力是对时间的平均力,而动能定理中的平均力是对位移的平均力。
【动量定理模型的建立】动量定理在流体、微粒类中的应用,关键是建立“柱状模型”,选择好△m和△t,并且建立好△m和△t的关系。
具体步骤:
1.研究△t时间内参与作用的流体:适用于流体运动过程中局部发生速度突变问题.
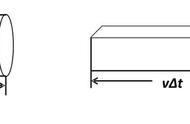
2.模型:处理截面积为S,长为v△t的小柱体(可以是圆柱体也可以是长方体)

3.△m的计算:△m=ρsv△t
4.作用过程:由于△t很小(△t→0),△m也很小,可看成物块与物体的碰撞.
例题:最大截面S=5m²的一艘宇宙飞船,以速度v=10km/s在太空中航行时,进入静止的、密度ρ=2×10⁻⁵kg/m³的微陨石云中.如果微陨石与飞船相撞时都附着在飞船上,要使飞船维持原速度前进,飞船的推力应为多大?

【审题指导】
1.在△t时间内,附着在飞船上的微陨石质量△m是多少,应如何求△m?
2.在△t时间内,落到飞船上的微陨石动量增加了多少?
【动量定理】以△t内的△m为研究对象:
F·△t=△m·△v
-F·△t=ρ·v·△t·S·(0-v)
【动能定理】
☞微元法是物理学上用来处理变质量问题时常用的思想方法.在本章中对这类有连续质量流动的问题,在应用动量定理时关键在于研究对象的选取,通常所采用的方法是选△t时间内发生相互作用的流体为研究对象,确定发生相互作用前后的动量.然后由动量定理解题。
例题:(两物体都在运动)一艘帆船在静水中由于风力的推动做匀速直线运动,帆面的面积为S,风速为v₁,船速为v₂(v₂<v₁),空气密度为ρ,帆船在匀速前进时帆面受到的平均风力大小为()。
A.ρS(v₁-v₂)
B.ρS(v₁²-v₂²)
C.ρS(v₁+v₂)²
D.ρS(v₁-v₂)²

例题:有一种灌浆机可以持续将某种涂料以速度v喷在墙壁上,其喷射出的涂料产生的压强为p,若涂料打在墙壁上后便完全附着在墙壁上,涂料的密度为ρ。则墙壁上涂料厚度增加的速度u为(B)
Α.ρp/v
B.p/ρv
C.ρ/pv
D.pv/ρ
例题:某风力发电机如图所示,

风力带动叶片转动,叶片再带动转子(磁极)转动,使定子(线圈,不计电阻)中产生电流,实现风能向电能的转化。已知叶片长为l,风速为v,空气的密度为ρ,空气遇到叶片旋转形成的圆面后一半减速为零,一半原速率穿过,下列说法正确的是( BС )
A一台风力发电机获得风能的功率为πρl²v³/2
B.一台风力发电机获得风能的功率为πρl²v³/4
C空气对一台风力发电机的平均作用力为πρl²v²/2
D.空气对一台风力发电机的平均作用力为πρl²v²/4
例题:某城市广场喷泉的喷嘴横截面为S,喷泉喷出的水柱超过了高度h。已知水的密度为ρ,重力加速度为g,则用于给喷管喷水的电动机输出功率至少为(B )
A. ρghS
B. ρghS√2gh
C. ρghS/2
D. ρghS√2gh/2
,