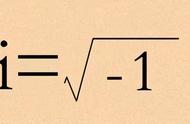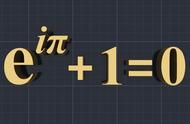正数的平方是正数,负数的平方也是正数,0的平方还是0,所以不可能存在一个数的平方等于-1。如果事实如此的话,那结果就不尽完美了,对于开方运算,实数并不具备封闭性。对于高次方程,结果可能是灾难性的。
数学家怎么会允许这样的遗憾发生,之前没有,并不代表不存在,就像负数一样,也许此刻我们眼中的虚数就像数百年前人眼中的负数一样。
1637年,法国数学家笛卡尔在《几何学》中说道:“负数开平方是不可思议”,并且他创造一名字“imaginary number”(虚数),意思为“虚幻之数”。但后来他改变了看法,正确认识了虚数的存在,把“虚幻之数”改为“虚数”,与“实数”相对应。“虚数”因此得名,沿用至今。
140年后,欧拉首次创用符号“i”来表示根号-1,即我们所说的虚数单位。

定义:i²=-1,形如:a bi(a≠0)的数叫做虚数,其中a,b是实数。
虚数与实数构成的集合叫做复数。复数的一般形式为:a bi
a叫做实数部分,bi称为虚数部分,当b=0时为实数,当a=0时称为纯虚数。
虽然有了虚数个概念,但虚数到底是什么?是不是只是纯粹臆想出来,照这么操作,是不是也可以定义一个w使得1/0=w?
我们先来解释其存在的合理性。
创造新的数的必要条件是,一定要适用于我们现有的运算系统。
考虑对任意两复数作加法,会有:

考虑对任意两复数作乘法,会有:

考虑对任意两复数作除法,会有: