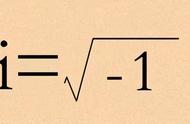对任意复数作开方,则其结果必然还是复数。
综合以上运算,可以发现,复数完全适用于我们的这套算法体系啊,甚至,还解决了对开方具有封闭性的这个问题。
反观为何不能定义w使得,如1/0=w果存在,则w 1=?,我们只能得到w 1=w,两边同减去w,得到1=0,what?所以这样的w无法存在。
05 再识虚数
实数我们都能够理解的一个主要原因是我们有一条叫做数轴的直线,每个实数对应数轴上的一个点,准确讲,这条轴应该叫实数轴,与此对应,其实也可以有虚数轴。
问:-1×(-1)=?
结果当然都知道,负负得正,所以结果等于1嘛。
再问:为什么负负得正?

提供一种思路,我们知道2×(-1)=-2,可以这么理解,所谓×(-1)就是将数轴上的数绕原点逆时针旋转180°。
2×(-1)便是将2绕原点转180°,其结果就是-2,-1×(-1)=1也是同样的道理,将-1这个点绕原点逆时针转动180°便得到1.

观察式子:1×i×i=-1,对1做两次×i的操作,结果为-1,相当于把1绕原点逆时针转了180°。
观察式子:1×i=i,对1做一次乘i的操作,得到的结果为i,那i在什么地方?
相当于把1绕原点逆时针转了90°!

一次转90°,两次转180°,所以有1×i×i=-1。
所以i所在的位置是一条与实数轴垂直的直线,我们称其为虚数轴。
是否觉得似曾相识,和平面直角坐标系是不是像得很?
实际上,高斯同学曾表示,既然复数a bi有数部和虚部两个部分,不如用符号(a,b)来表示,(a,b)是一组有序数对,每一个(a,b)对应一个复数。