统计量u和t是什么意思,统计中的t代表什么

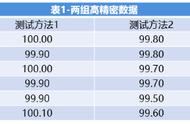
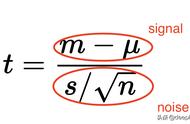我们之前文章里介绍的卡方检验运用于分类数据的问题，数据是离散的。今天我们要讨论有关连续性数据的检验问题，是与最重要的正态分布有关的。

我们使用例子：工厂供给用户一种产品，要求的规格是每袋100千克。现用户对这项规格是否达到有怀疑，决定抽取若干袋进行检查，来看看这种怀疑是否有根据。

若以X记从该厂随机抽取的一袋产品的重量，则X为随机变量。检验步骤如下：

（1）设定如下前提

1） 假定X服从正态分布，这形式上是一个纯粹的数学性假定，但正如我们以前文章里介绍正态分布时提到的，它有一定的理论和经验上的根据

2） 在X~N(a,σ^2)的前提下，我们把要检验的原假设表示为：a=100(首先，因有随机因素的干扰，不论厂方主观上如何努力，也不能做到每袋恰为100千克，因此，所提规格应解释为:X的均值为100(千克)；另外，原假设不表示为a不等于100，是因为在没有实地检查前不好先天地认为它不合规格，且在正常情况下，厂方也会努力做到合规格。因此，在得出“不合规格”的结论时，应当更为慎重)

（2）抽样并在原假设的前提下算出样本的拟合优度（对于拟合优度以及检验水平的解释详见卡方检验一章）

设从工厂产品中抽取n袋，以x₁，…，x_n记它们的重量，则`x＝∑x<sub>i</sub>/n是均值a的良好估计。若原假设成立，则a＝100，故|`x-100|应倾向于小。因此，我们自然地把那些满足条件

的样本(X₁，…，X_n)看作比`x更背离原假设。在原假设下算出这些样本的概率，即为样本的拟合优度。则

(3)假定方差已知。使用u检验法

因为

有标准正态分布，记此变量为Y～N(0,1)。则拟合优度的计算式可改写为