三角形是初中平面几何学习中最重要的一个基本平面图形,很多复杂的平面图形问题都需要转化为三角形来进行处理,同样它也是三角函数知识与平面几何知识的交汇点,因此,在高中数学教学中要求学生对于三角形中的基本概念和基本方法必须全盘熟练掌握。然而初中阶段对于三角形的教学要求明显不能切合高中教学,很多概念和方法没能进行详细介绍,这里我们重点来讲一讲三角形的“五心”。
什么是三角形的“五心”?通常我们把三角形的外心、内心、重心、垂心和旁心,称之为三角形的“五心”,这“五心”是三角形中特殊直线的交点,也是三角形中各种重要性质的源点。下面我们就来逐一了解一下这“五心”及其应用。
首先我们来看一下三角形的外心,三角形的外心是三角形外接圆的圆心,也是三角形三边中垂线的交点。它是初中平面几何当中比较重点介绍的一个知识点,与三角形外心比较密切的有圆心角和圆周角定理。通过作图我们很容易发现,锐角三角形的外心在三角形内,钝角三角形的外心在三角形外,直角三角形的外心是斜边的中点。

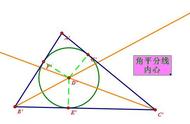
接下来我们来看一下三角形的内心,三角形的内心是三角形内切圆的圆心,也是三角形三条角平分线的交点。在初中平面几何的学习中这个知识点也已经做了比较详细的介绍,与之相关的主要是三角形角平分线的一些性质,以及圆的切线、割线相关的一些性质。三角形的内心一定在三角形内部,并且到三边距离相等。特别的,直角三角形内心到边的距离(内切圆半径)等于两直角边之和与斜边差的一半。

再接下来我们来看一下三角形的重心,三角形的重心是三角形三条中线的交点。在初中平面几何的学习中对这部分内容基本没有介绍,但这部分内容却是高中数学学习中不可缺少的重要内容。对于三角形的重心,我们必须要了解的性质如下:1)三角形的重心是每条中线的三等分点(用相似三角形知识即可轻松证明);2)三角形的重心与三角形三个顶点的连线三等分三角形的面积;3)三角形的重心到三角形三个顶点距离的平方和最小。

下面我们再说一说三角形的垂心,三角形的垂心是三角形三条高线的交点。初中平面几何几乎没有谈及这方面概念,但三角形垂心的概念和性质在高中阶段的数学学习中时常涉及,对于垂心,我们需要了解的性质主要有:1)垂心分每条高线的两部分乘积相等;2)垂心到三角形任一顶点的距离等于外心到这个顶点对边距离的两倍;3)三角形外心、重心、垂心三点共线(欧拉线),重心分外心与垂心连线段之比为1:2。

最后我们来看一下三角形的旁心,三角形的旁心是三角形旁切圆的圆心,也是三角形一个内角平分线与不相邻的两个外角平分线的交点。不同于其他“四心”,三角形旁心有三个,每一个到三角形三边距离都相等。旁心的问题在高中数学学习中很少见到,通常只在竞赛问题中出现,因此简单了解其概念即可。
,