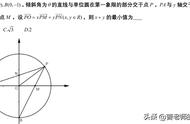
图形三
在直观上,切线给我们它与曲线“擦肩而过”的感觉!割线给我们它与曲线“穿身而过”的印象!
在教学中,有同学说,切线也可以这样定义:如果直线与曲线有且只有一个公共点,那么称这条直线是曲线的切线。
这种说法对不对呢?我们可以再看看上面图形二中的切线。
我们看到,这条切线与曲线的公共点就有两个。
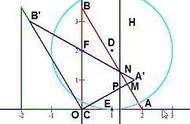
事实上,切线与曲线公共点的个数是与曲线本身和切线的位置有关,而且还可能出现切线与曲线有多个以上公共点的情形,如下图四,直线与曲线相切就有三个公共点,当然,切点是只有一个,其它是普通的交点。

图形四
当然,直线与曲线相切时只有一个公共点(就是切点)的情形也有,比如我们熟悉的直线与圆相切,直线与椭圆相切。如图形五,图形六:

图形五

图形六
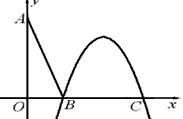
通过上面的图形演示我们知道了,相切时可以有多个公共点 ,那么,反过来,如果直线与曲线只有一个公共点,那么直线与曲线一定相切吗?我们看下面的图七直线与抛物线的位置关系的演示: