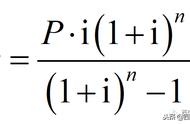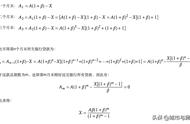银行贷款常见还款方式利息计算
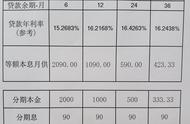
银行贷款最常见的还款方式有等额本金,等额本息,先息后本,随借随还等,今天咱们聊一聊等额本金的利息计算。
等额本金还款方式
每月还款的本金固定不变,利息递减。利息随着本金的减少而减少,根据剩余本金来结算下个月的利息。
优点:总利息较少;提前还款灵活
缺点:初期还款压力较大

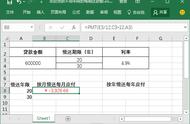
月利息计算公式:
每月利息 = 剩余未偿还本金 * 月利率。
从这个公式可以看出等额本金每月利息随着本金的减少而减少。
总利息计算公式:

总利息 = (贷款总额 * 月利率 * (还款期数 1)) / 2
这个公式是由总利息 = 第一个月的利息 第二个月的利息 ... 第 n 个月的利息公式推导而来,下面是推导过程
设贷款总额为 P,月利率为 R,还款期数为 n,每个月的本金还款额为 A。
由于等额本金方式下,每个月的本金还款额相同,所以第一个月的本金还款额为 A,第二个月的本金还款额也为 A,依此类推,第 n 个月的本金还款额也为 A。
对于每个月的利息,我们可以通过以下方式计算:
第一个月的利息:P * R
第二个月的利息:(P - A) * R
第三个月的利息:(P - 2A) * R
第四个月的利息:(P - 3A) * R
……
第 n 个月的利息:(P - (n-1)A) * R
可以观察到,每个月的利息都是通过剩余未偿还本金乘以月利率得到的。
总利息是每个月利息的累加,即:
总利息 = 第一个月的利息 第二个月的利息 ... 第 n 个月的利息
可以整理为:
总利息 = (P *R) ((P - A) *R) ((P - 2A) *R) ... ((P - (n-1)A) *R)
因为等额本金还款方式下,贷款总额 P 是固定的,每个月的本金还款额 A 也是固定的,所以可以提取公因式R,并将上式简化为:
总利息 =R* (P (P - A) (P - 2A) ... (P - (n-1)A))
=R*(nP -(A 2A 3A … (n-1)A)
=R*(nP – A(1 2 3 … (n-1))
1 2 3 … (n-1)是公差为1,项数为n-1的等差数列
等差数列求和公式为:Sn = (n/2) * (a l)
根据上面的求和公式,我们可以将总利息进一步简化为:
总利息 = (2RnP – Ran^2 Ran)/2
因为每月本金是一样的,所以总额P=An
化简得到:
总利息 =(2RnP –RnP RP)/2
=(PR(n 1))/2
= (贷款总额 * 月利率 * (还款期数 1)) / 2
这就是等额本金总利息的推导过程。
等额本金还款方式适用人群
1、财务状况相对稳定的借款人:等额本金还款方式要求借款人每个月偿还相同的本金金额,这意味着在还款期限内需要有稳定的收入来源来承担前期的还款压力。
2、希望尽快还清贷款的借款人:等额本金还款方式在每个月的本金还款额相同的情况下,每个月的利息支出逐渐减少,从而减少了总利息支出。这种方式适合那些希望尽快偿还贷款并减少贷款总成本的借款人。
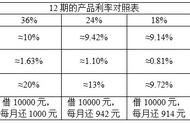
3、对贷款利息敏感的借款人:等额本金还款方式相比于其他还款方式(如等额本息),在还款期限内减少了总利息支出。对于那些对贷款利息敏感,希望减少贷款成本的借款人来说,等额本金是一个较为合适的选择。
4、理财能力较强的借款人:等额本金还款方式在初期的还款额较大,可能对借款人的现金流造成一定的压力。因此,适用于具备一定理财能力,能够在还款期间进行有效的资金管理,以确保每月能够按时支付本金和利息的借款人。
需要注意的是,借款人在选择还款方式时应根据个人财务状况、预期还款能力和偏好进行综合考虑。等额本金还款方式适用于一些特定情况,但并不适用于所有借款人。在做出决策之前,建议咨询专业金融顾问或与贷款机构进行详细讨论。
,