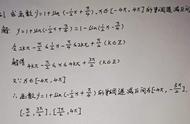通过对全国各地高考数学试卷进行分析和研究,我们发现与三角函数、三角恒等变换和解三角形等有关的试题,一直是高考数学必考的热点。
对于三角函数这部分内容,高考数学除了考查基础知识和方法技巧之外,更加注重化归与转化的思想方法的渗透,注重整体思想的运用,注重与其他知识的综合等。
遇到三角函数类问题,一般是先进行恒等变换,再利用三角函数图象和性质进行解题。因此,考生在复习期间,要掌握好三角函数的图像与性质,深刻理解相关的性质定理,提高分析问题和解决问题的能力,特别是要努力去提高演绎推理能力、计算能力、综合应用知识解决问题的能力,这些都是高考数学重点考查对象。

大家要记住:高考考的不仅仅是一个人掌握多少知识内容,更主要考查一个人运用知识的能力。
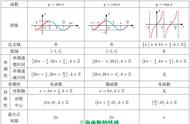
周期性是函数的整体性质,要求对于函数整个定义域内的每一个x值都满足f(x+T)=f(x),其中T是不为零的常数.如果只有个别的x值满足f(x+T)=f(x),或找到哪怕只有一个x值不满足f(x+T)=f(x),都不能说T是函数f(x)的周期。
因此,学好三角函数的图像与性质,就要先掌握好周期函数这一概念。
什么是周期函数的定义?
对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数。
T叫做这个函数的周期。

已知函数f(x)=(sinx-cosx)sin2x/sinx.
(1)求f(x)的定义域及最小正周期;
(2)求f(x)的单调递增区间.
解:(1)由sin x≠0得x≠kπ(k∈Z),
故f(x)的定义域为{x∈R|x≠kπ,k∈Z}.
因为f(x)=(sinx-cosx)sin2x/sinx
=2cos x(sin x-cos x)
=sin 2x-cos 2x-1
=√2sin(2x-π/4)-1,
所以f(x)的最小正周期T=2π/2=π.
(2)函数y=sin x的单调递增区间为[2kπ-π/2,2kπ π/2]
(k∈Z).
由2kπ-π/2≤2x-π/4≤2kπ+π/2,x≠kπ(k∈Z),
得kπ-π/8≤x≤kπ+3π/8,x≠kπ(k∈Z).
所以f(x)的单调递增区间为[kπ-π/8,kπ)和(kπ,kπ 3π/8](k∈Z).

求三角函数的单调区间时,应先把函数式化成y=Asin(ωx+φ)(ω>0)的形式,再根据三角函数的单调区间,求出x所在的区间.应特别注意,考虑问题应在函数的定义域内。
注意区分下列两种形式的函数单调性的不同。
三角函数的图像与性质,典型例题分析2:已知函数f(x)=2sin(π-x)cos x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间[-π/6,π/2]上的最大值和最小值.
解:(1)∵f(x)=2sin(π-x)cos x=2sin xcos x=sin 2x,
∴函数f(x)的最小正周期为π.
(2)∵-π/6≤x≤π/2,
∴-π/3≤2x≤π,
则-√3/2≤sin 2x≤1.
所以f(x)在区间[-π/6,π/2]上的最大值为1,最小值为-√3/2.