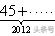XX 外国语学校分班考试数学试卷
一、用心思考,正确填写:(每题 2 分,共 40 分)
1.(2 分) 立方米= _________ 立方分米;8 点 12 分= _________ 时.
2.(2 分)在 73.5%, ,0.7255,0.7 中,最大的数是 _________ ,最小的数
是 _________ .
3.(2 分)50 千克增加 _________ %是 80 千克,比 _________ 千克多 是 60 千克.
4.(2 分)甲乙两家汽车销售公司根据近几年的销售量分量制作如图统计图:
从 2004 年到 2008 年,这两家公司中销售量增长较快的是 _________ 公司.(填甲或乙)
5.(2 分)一辆汽车从甲地开往乙地用了 5 小时,返回时速度提高了 20%,这样少用了 _________
小时.
6.(2 分)有一个分数约成最简分数是 ,约分前分子分母的和等于 48,约分前的分数是
_________ .
7.(2 分)把一个圆柱体侧面展开,得到一个正方形,这个圆柱体底面半径是 0.5 分米,圆柱体的高
是 _________ 分米.
8.(2 分)一个圆锥形沙堆,底面积是 314 平方米,高 1.5 米.用这堆沙填一条宽 10 米的公路,要
求填 5 厘米厚,能填多远?
9.(2 分)淘宝商城为了增加销售额,推出"五月销售大酬宾"活动,其活动内容为"凡五月份在该商
城一次性购物超过 50 元以上者,超过 50 元的总分按 9 折优惠",在大酬宾活动中,李明在该商城为
班级购买了单价为 30 元的学习用品 X 件,(X>2),则应付货款 _________ 元.
10.(2 分)a、b、c、d 是四个不同的自然数,且 a×b×c×d=2790,a b c d 最小是 _________ .
11.(2 分)如图中两个正方形面积之差为 400 平方厘米,那么两圆的面积之差为 _________ 平方
厘米.(圆周率取 3.14)
12.(2 分)某超市运来一批货物,其中有土豆 2000 千克,东瓜 800 千克,芹菜 700 千克,番茄若干,
用扇形统计图表示如图所示,则番茄有 _________ 千克.
13.(2 分)一个直圆锥的体积是 120 立方厘米,将圆锥体沿高的 处横截成圆台,将这个圆台放入圆
柱形纸盒,纸盒的容积至少是 _________ 立方厘米.
14.(2 分)如果 ab=21,a﹣b=4,(a﹣b)2=a2﹣2ab b2,那么 a2 b2 2= _________ .
15.(2 分)有两根长短粗细不同的蚊香,短的一根可燃 8 小时,长的一根可燃时间是短的 ,同时点
燃两根蚊香,经过 3 小时,它们的长短正好相等,未点燃之前,短蚊香比长蚊香短 _________ .
16.(2 分)已知图中△ ABC 的每边长都是 96cm,用折线把这个三角形分割成面积相等的四个三角
形,则线段 CE 和 CF 的长度之和为 _________ cm.
17.(2 分)某班一次考试的平均分数是 70 分,其中 的人及格,他们的平均分是 80 分,则该班不及
格的人的平均分是 _________ 分.
18.(2 分)中央电视台二套"开心辞典"是一档广受大家喜爱的节目,某期有这样一个问题:如图所
示,两个天平都平衡,根据图象回答三个球体的重量等于 _________ 个正方体的重量.
19.(2 分)有一种用来画圆的工具板(如图所示),工具板长 21cm,上面依次排列着大小 不等的五
个圆孔,其中最大圆的直径为 3cm,其余圆的直径从左到右依次递减 0.2cm,最大圆的左侧工具板边
缘 1.5cm,最小圆的左侧距工具板右侧边缘 1.5cm,相邻两圆的间距 d 均相等,则相邻两圆的间距是
_________ cm.
20.(2 分)一个质数如果加上 3 能被 2 整除,加上 2 能被 3 整除,在 40 以内符合条件的质数共有
_________ 个.
二、反复比较,慎重选择(每小题 2 分,共 10 分)
21.(2 分)下面图形是用木条钉成的支架,最不容易变形的时( )
A.
B.
C.
D.
22.(2 分)一个真分数,它的分子、分母同时加上一个相同的非零自然数后,所得到的新分数一定
( )
A. 与原数相等 B. 比原数大 C. 比原数小 D. 无法确定
23.(2 分)随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费按原标准每分钟降低了 a 元
后,再次下调了 25%,现在的收费标准是每分钟 b 元,则原收费标准每分钟为( )元.
A. b﹣a B. b a C. b a D. b a
24.(2 分)四个同样大小的圆柱拼成一个高为 40 厘米的大圆柱时,表面积减少了 72 平方厘米,原
来小圆柱的体积是( )立方厘米.
A. 120 B. 360 C. 480 D. 720
25.(2 分)图 1 是一个三角形,沿虚线折叠后得到图 2,这个多边形的面积是原三角形面积的 .已
知图 2 中阴影部分的面积和为 15 平方厘米,那么原三角形的面积是( )平方厘米.
A. 26 B. 27 C. 28 D. 29
三、仔细推敲,辨析正误.(每题 1 分,共 5 分)
26.(1 分)一个三角形,两内角之和是 91°,它一定是锐角三角形. _________ .
27.(1 分)两个自然数的积一定是合数. _________ .
28.(1 分)通过放大镜看一个 20°的角,这个角仍是 20°. _________ .
29.(1 分)一个小数的倒数一定比原来的小数大. _________ .
30.(1 分)正方体棱长扩大 2 倍,它的表面积就扩大 8 倍,它的体积也扩大 8 倍. _________ .
四、看清题目,巧思妙算:(共 44 分)
31.(16 分)
直接写数对又快:
(1)47.23﹣(7.23 5.89)= (2) ﹣ ﹣ = (3)12.5×8.8÷11= (4)( )×12=
(5) × 40%× = (6) ÷5 5÷ = (7)99 999 9999 99999= (8) × 1.25× 125%=
32.(20 分)神机妙算(能简算的要写出简算过程)
(1) … =
(2)( × )÷(1﹣ )=
(3)3.5÷ 6.5×[12×( ﹣0.3)﹣15%
(4)已知: = = =20092010,求 的值.
(5) … .
33.(8 分)巧解密码:
(1)(3X 2) 2[(X﹣1)﹣(2X 1)]=6
(2)若 X:7.5=0.16: ,求 75X 8 的值.
五、图形题:(每题 4 分,共 8 分.)
34.(5 分)如图是边长 6 米的正方形和梯形拼成的"火炬",梯形的上底长 9 米,A 为上底的中点,B
为下底的中点,线段 AB 恰好是梯形的高且长为 3 米,CD 长为 2 米,那么,图中阴影部分的面积是
多少平方米?
35.(6 分)有一个电动玩具,它有一个 8.28×5.14 的长方形盘(单位:厘米)和一个半径为 1 厘米的
小圆盘(盘中画有娃娃脸)它们的连接点为 A、B(如图)如果小圆盘沿着长方形内壁,从 A 点出发,
不停的滚动(无滑动),最后回到原来位置,请你计算一下,小圆盘(娃娃脸)在 B、C、D 位置是
怎样的,并请画出示意图?小圆盘共自转了几圈?
36.(6 分)已知一串分数: , , , , , , , , , …
(1) 是此串分数中的第多少个分数?
(2)第 115 个分数是多少?
37.(10 分)已知甲从 A 到 B,乙从 B 到 A,甲、乙二人行走速度之比是 6:5.如图所示 M 是 AB
的中点,离 M 点 26 千米处有一点 C,离 M 点 4 千米处有一点 D.谁经过 C 点都要减速 ,经过 D
点都要加速 ,现在甲、乙二人同时出发,同时到达.求 A 与 B 之间的距离是多少千米?
38.(14 分)材料:股票市场,买、卖股票都要分别交纳印花税等有关税费,以泸市 A 股的股票交
易为例,除成本外还要交纳:
(1)印花税:按成交金额的 0.1%计算;
(2)过户费:按成交金额的 0.1%计算;
(3)佣金:按不高于成交金额的 0.3%计算,不足 5 元按 5 元计算.
问题:(1)小王以每股 5.00 元的价格买入股票"美的电器"100 股,以每股 5.50 元的价格全部卖出,
则他盈利为 _________ 元.
(2)小张以每股 A 元(A≥5)的价格买入以上股票,股市波动大,他准备在不亏不盈时卖出,请你
帮他计算卖出的价格每股是 _________ 元(用 A 的代数式表示).由此可得卖出价格与买入价格
相比至少要上涨(%)才不亏(结果保留三个有效数字)
(3)小张再以每股 5.00 元的价格买入以上股票 1000 股,准备盈利 1000 元时才卖出,请你帮他计算
卖出的价格每股是多少元?
外国语学校分班考试数学试卷
参考答案与试题解析
一、用心思考,正确填写:(每题 2 分,共 40 分)
1.(2 分) 立方米= 8750 立方分米;8 点 12 分= 8 时.
考点: 体积、容积进率及单位换算;时、分、秒及其关系、单位换算与计算。522571
分析: ①把 8 立方米化成立方分米数,用 8 乘进率 1000;
②把 8 点 12 分化成时数,首先把 12 分化成时数,用 12 除以进率 60,然后再加上 8,即可得
解.
解答: 解:①8 ×1000=8750(立方分米),
所以 立方米=8750 立方分米;
②12÷60 8=8 (时),
所以 8 点 12 分=8 时;
故答案为:8750,8 .
点评: 此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,反之,
则除以进率.
2.(2 分)(2012•长寿区)在 73.5%, ,0.7255,0.7 中,最大的数是 ,最小的数是 0.7 .
考点: 小数大小的比较;小数、分数和百分数之间的关系及其转化。522571
分析: 有几个不同形式的数比较大小,一般情况下,都化为小数进,把循环小数简写形式写成一般
形式行比较得出答案.
解答: 解:73.5%=0.735, ≈0.7778,0.7 =0.7252525…,
0.7778>0.735>0.7255>0.72525…,
所以最大的数是 0.7778 即 ,最小的数是 0.72525…即 0.7 ;
故答案为: ,0.7 .
点评: 解决有关小数、百分数、分数之间的大小比较,一般都把分数、百分数化为小数再进行比较,
从而解决问题.
3.(2 分)50 千克增加 60 %是 80 千克,比 50 千克多 是 60 千克.
考点: 百分数的加减乘除运算;分数除法。522571
分析: (1)把 50 千克看成单位"1",用 80 千克减去 50 千克求出需要增加的重量,然后再除以 50
千克即可.
(2)把要求的数量看成单位"1",它的(1 )对应的数量是 60 千克,由此用除法求出要求
的数量.
解答: 解:(1)(80﹣50)÷50,
=30÷50,
=60%;
(2)60÷(1 ),
=60 ,
=50(千克);
故答案为:60,50.
点评: 此题考查的是简单的分数应用题,要先找准单位"1",再据题中的数量关系列式求解.
4.(2 分)甲乙两家汽车销售公司根据近几年的销售量分量制作如图统计图:
从 2004 年到 2008 年,这两家公司中销售量增长较快的是 甲 公司.(填甲或乙)
考点: 单式折线统计图。522571
分析: 结合折线统计图中的数据,分别求出甲、乙各自的增长量即可求出答案.
解答: 解:从折线统计图中可以看出:
甲公司 2008 年的销售量约为 620 辆,2004 年约为 180 辆,则从 2004~2008 年甲公司增长了
620﹣180=440 辆;
乙公司 2008 年的销售量为 400 辆,2004 年的销售量为 150 辆,
则从 2004~2008 年,乙公司中销售量增长了 400﹣150=250 辆.
则甲公司销售量增长的较快.
故答案为:甲公司.
点评: 本题考查了折线统计图,单纯从折线的陡峭情况来判断,很易错选乙公司;但是两幅图中横
轴的组距选择不一样,所以就没法比较了,因此还要抓住关键.
5.(2 分)一辆汽车从甲地开往乙地用了 5 小时,返回时速度提高了 20%,这样少用了 小时.
考点: 简单的行程问题;百分数的实际应用。522571
分析: 设汽车速度为 x,则甲乙两地距离为 5x,返回时速度提高 20%,则提高后速度为(1 20%)
x=1.2x,所以.返回时用时为 =4 ,所以少用了 5﹣4 = .
解答: 解:设汽车速度为 x,则甲乙两地距离为 5x,返回时用时为:
=4 ,
所以少用了 5﹣4 = .
答:这样少用了 小时.
故答案为: .
点评: 通过设未知数,根据路程÷速度=时间得出提高速度后所用时间是完成本题的关键.
6.(2 分)有一个分数约成最简分数是 ,约分前分子分母的和等于 48,约分前的分数是 .
考点: 分数的基本性质。522571
分析: 已知有一个分数约成最简分数是 ,可以理解为分子与分母的比是 5:11,约分前分子分母的
和等于 48,原来的分子占分子分母和的 ,原来的分母占分子分母和的 ,根据一个数
乘分数的意义,用乘法解答.
解答: 解:原来的分子是:
48× ,
=48× ,
=15;
原来的分母是:
48× ,
=48× ,
=33;
答:约分前的分数是 .
故答案为: .
点评: 此题主要考查分数的基本性质的应用,解答关键是把分数转化成比,利用按比例分配的方法
即可求出原来的分数.
7.(2 分)(2012•长寿区)把一个圆柱体侧面展开,得到一个正方形,这个圆柱体底面半径是 0.5 分
米,圆柱体的高是 3.14 分米.
考点: 圆柱的展开图。522571
分析: 因为该圆柱的侧面展开后是正方形,根据"圆柱的侧面展开后是一个长方形,长方形的长等于
圆柱的底面周长,长方形的宽等于圆柱的高"可知:该圆柱是底面周长和高相等,即圆柱的底
面周长等于正方形的边长,因为圆柱的底面是圆形,根据"C=2πr"解答即可.
解答: 解:2×3.14×0.5,
=6.28×0.5,
=3.14(分米);
答:这个正方形的边长是 3.14 分米;
故答案为:3.14.
点评: 抓住展开图的特点得出高与底面周长的关系是解决本题的关键.
8.(2 分)一个圆锥形沙堆,底面积是 314 平方米,高 1.5 米.用这堆沙填一条宽 10 米的公路,要
求填 5 厘米厚,能填多远?
考点: 关于圆锥的应用题。522571
分析: 根据圆锥的体积公式,先求圆锥形沙堆的体积,再根据沙子的体积不变,利用长方体的体积
公式变形,即可求出所填路的长度.
解答: 解:5 厘米=0.05 米,
×314×1.5÷(10×0.05),
=157÷0.5,
=314(米);
答:能填 314 米.
点评: 此题主要考查了圆锥和长方体的体积公式在实际生活中的应用.
9.(2 分)淘宝商城为了增加销售额,推出"五月销售大酬宾"活动,其活动内容为"凡五月份在该商
城一次性购物超过 50 元以上者,超过 50 元的总分按 9 折优惠",在大酬宾活动中,李明在该商城为
班级购买了单价为 30 元的学习用品 X 件,(X>2),则应付货款 27x 5 元.
考点: 百分率应用题。522571
分析: 根据题意,可先求出购买的学习用品超过 50 元的那部分钱数,再求出超过的这部分钱数打 9
折实际应花的钱数,进而再加上 50 元即可.
解答: 解:50 (30x﹣50)×0.9,
=50 27x﹣45,
=27x 5;
答:则应付货款 27x 5 元.
故答案为:27x 5.
点评: 此题考查百分率应用题,解决关键是先求出超过 50 元的那部分货款按 9 折优惠应付的钱数,
进而再加上 50 元.
10.(2 分)a、b、c、d 是四个不同的自然数,且 a×b×c×d=2790,a b c d 最小是 45 .
考点: 数字和问题。522571
分析: 由于 a、b、c、d 是四个不同的自然数,且 a×b×c×d=2790,因此可先将 2790 分解质因数,
2790=2×3×3×5×31,所以 2790 含有 5 个质因数,这些质因数中,只有 2×3=6 的值最小,所以
这四个因数可为 3×6×5×32=2790,则 a b c d 最小是 3 5 6 31=45.
解答: 解:由于 2790=2×3×3×5×31,
只有 2×3=6 的值最小,a×b×c×d=3×6×5×32=2790,
则 a b c d 最小是 3 5 6 31=45.
故答案为:45.
点评: 先根据题意将 2790 分解质因数,再根据其质因数的情况进行分析是完成本题的关键.
11.(2 分)如图中两个正方形面积之差为 400 平方厘米,那么两圆的面积之差为 314 平方厘米.(圆
周率取 3.14)
考点: 圆、圆环的面积;长方形、正方形的面积。522571
分析: 设大正方形的边长为 a 厘米,小正方形的边长为 b 厘米,则大正方形的面积为 a2平方厘米,
小正方形的面积为 b2 平方厘米,再根据"两个正方形面积之差为 400 平方厘米",所以 a2﹣
b2=400 平方厘米,从图中知道大圆的半径是 厘米,小圆的半径是 厘米,由此知道大圆的面
积是 ×π= ×π 平方厘米,小圆的面积是 ×π= ×π,由此即可求出两圆的面积之
差.
解答: 解:设大正方形的边长为 a 厘米,小正方形的边长为 b 厘米,则大正方形的面积为 a2平方厘
米,小正方形的面积为 b2 平方厘米,
a2﹣b2=400 平方厘米
大圆的面积与小圆的面积的面积差是: ×π﹣= ×π,
= (a2﹣b2),
= ×3.14×400,
=314(平方厘米),
答:两圆的面积之差为 314 平方厘米,
故答案为:314.
点评: 关键是根据图找出正方形的边长与圆的半径的关系,结合题意利用正方形的面积公式与圆的
面积公式解决问题.
12.(2 分)某超市运来一批货物,其中有土豆 2000 千克,东瓜 800 千克,芹菜 700 千克,番茄若干,
用扇形统计图表示如图所示,则番茄有 875 千克.
考点: 百分数的实际应用。522571
分析: 由图可知:把总重量看成单位"1",番茄占总重量的 20%,其它一共占总重量的(1﹣20%),
它对应的数量是(2000 800 700)千克;由此用除法求出总重量,用总重量乘 20%就是番茄
的重量.
解答: 解(2000 800 700)÷(1﹣20%),
=3500÷80%,
=4375(千克);
4375×20%=875(千克);
答:番茄有 875 千克.
故答案为:875.
点评: 本题的关键是找出单位"1",并找出数量对应的单位"1"的百分之几,用除法就可以求出单位"1"
的量;求单位"1"的百分之几用乘法.
13.(2 分)一个直圆锥的体积是 120 立方厘米,将圆锥体沿高的 处横截成圆台,将这个圆台放入圆
柱形纸盒,纸盒的容积至少是 180 立方厘米.
考点: 圆锥的体积。522571
分析: 根据题干可知,要求这个纸盒的容积至少值,则这个圆柱形容器的高是圆锥的高的 ,底面积
与圆锥的底面积相等,由此利用圆柱与圆锥的体积公式先求出它们的体积之比即可解答.
解答: 解:设圆锥的高是 2h,则圆柱的高是 h;它们的底面积是 S,
所以圆锥的体积是: ×S×2h= Sh;
圆柱的体积是:Sh;
则圆锥与圆柱的体积之比是: Sh:Sh=2:3,
因为圆锥的体积是 120 立方厘米,所以圆柱的体积是:120×3÷2=180(立方厘米),
答:纸盒的容积至少是 180 立方厘米.
故答案为:180.
点评: 此题考查了圆柱与圆锥的体积公式的灵活应用.
14.(2 分)如果 ab=21,a﹣b=4,(a﹣b)2=a2﹣2ab b2,那么 a2 b2 2= 60 .
考点: 含字母式子的求值。522571
分析: 先将 a2 b2 2 变形为(a﹣b)2 2ab 2,再整体代入即可求解.
解答: 解:因为 ab=21,a﹣b=4,
则 a2 b2 2
=(a﹣b)2 2ab 2
=42 21×2 2
=16 42 2
=60.
故答案为:60.
点评: 考查了含字母式子的求值,本题的关键是根据(a﹣b)2=a2﹣2ab b2,把 a2 b2 2 变形得到(a
﹣b)2﹣2ab 2,同时注意整体思想的运用.
15.(2 分)有两根长短粗细不同的蚊香,短的一根可燃 8 小时,长的一根可燃时间是短的 ,同时点
燃两根蚊香,经过 3 小时,它们的长短正好相等,未点燃之前,短蚊香比长蚊香短 .
考点: 分数四则复合应用题。522571
分析: 由"短蚊香可燃 8 小时,长蚊香可燃的时间是短蚊香的 "可知:长蚊香可燃的时间是 8× =4 小
时,每小时短蚊香用去 ,每小时长蚊香用去 ; 再由"同时点燃两根蚊香,经过 3 小时,它
们的长短正相等"可知:短蚊香的 8﹣3 小时长可燃的长度相当于长蚊香的 4﹣3 小时长可燃的
长度,即短蚊香长度的 相当于长蚊香长度的 ,由此进行解答.
解答: 解:有题意可知:
长蚊香可燃的时间是 8× =4(小时),
短蚊香长度×(1﹣ ×3)=长蚊香长度×(1﹣ ×3)
即短蚊香长度:长蚊香长度=(1﹣ ×3):(1﹣ ×3)= : = ,
所以短蚊香比长蚊香短(5﹣2)÷5= ;
故答案为: .
点评: 解此题要认真审题,关键是从"同时点燃两根蚊香,经过 3 小时,它们的长短正好相等"入手,
找到等式,解出短蚊香长度与长蚊香长的比.
16.(2 分)已知图中△ ABC 的每边长都是 96cm,用折线把这个三角形分割成面积相等的四个三角
形,则线段 CE 和 CF 的长度之和为 100 cm.
考点: 三角形的周长和面积。522571
分析: 根据三角形 ABC 的边长都是 96 厘米,用折线把三角形分割成面积相等的四个三角形,可得
△ ABD 和△ BDC 的面积之比是 1:3,根据三角形的高一定时,面积与底成正比的性质可得:
AD:DC=1:3;因为 AC=96 厘米,即可求得 CD=96× =72 厘米;同理即可求得 CF 和 CE 的
长度.
解答: 解:根据题干可得:△ ABD=△ BDE=△ DEF=△ EFC
(1)△ ABD 和△ BDC 的面积之比是 1:3,根据三角形的高一定时,面积与底成正比的性质
可得:AD:DC=1:3;因为 AC=96 厘米,即可求得 CD=96× =72 厘米;
(2)△ DEF 和△ EFC 的面积之比是 1:1,根据三角形的高一定时,面积与底成正比的性质
可得:DF:FC=1:1;因为 DC=72 厘米,即可求得 CF=72× =36 厘米;
(3)△ BDE 和△ EDC 的面积之比是 1:2,根据三角形的高一定时,面积与底成正比的性质
可得:BE:EC=1:2;因为 BC=96 厘米,即可求得 CE=96× =64 厘米;
所以 64 36=100(厘米);
答:线段 CE 和 CF 的长度之和为 100 厘米.
故答案为:100.
点评: 此题反复考查了三角形的高一定时,三角形的面积与底成正比的性质的灵活应用.
17.(2 分)某班一次考试的平均分数是 70 分,其中 的人及格,他们的平均分是 80 分,则该班不及
格的人的平均分是 40 分.
考点: 平均数问题。522571
分析: 假设某班有 n 人,用全班的总分 70n 减去及格人数的总分 n×80 就是不及格人的总分,不及
格人的总分除以不及格人数(n﹣ n)就是不及格人的平均分数.
解答: 解:假设某班有 n 人,则:
不及格人的平均分数为
(70n﹣ n×80)÷(n﹣ n)
=10n÷ n
=40(分).
答:该班不及格的人的平均分是 40 分.
故答案为:40.
点评: 考查了平均数问题,本题的关键是得到不及格人的总分和不及格人数,这是本题的难点.
18.(2 分)中央电视台二套"开心辞典"是一档广受大家喜爱的节目,某期有这样一个问题:如图所
示,两个天平都平衡,根据图象回答三个球体的重量等于 5 个正方体的重量.
考点: 简单的等量代换问题。522571
分析: 根据图中第一个天平知道:2 个球的重量=5 个砝码的重量,即 2×3 个球的重量=5×3 个砝码的
重量,根据图中第二个天平知道:2 个正方体的重量=3 个砝码的重量,即 2×5 个正方体的重
量=3×5 个砝码的重量,由此即可得出球体与正方体的关系,进而得出答案.
解答: 解:因为 2 个球的重量=5 个砝码的重量,
所以 2×3 个球的重量=5×3 个砝码的重量,
即 6 个球的重量=15 个砝码的重量;
又因为 2 个正方体的重量=3 个砝码的重量,
所以 2×5 个正方体的重量=3×5 个砝码的重量,
即 10 个正方体的重量=15 个砝码的重量;
所以 6 个球的重量=10 个正方体的重量,
6÷2 个球的重量=10÷2 个正方体的重量,
即 3 个球的重量=5 个正方体的重量;
故答案为:5.
点评: 关键是根据图列出数量关系等式,再根据等式的特点,选择的合适的运算方法,适时的进行
等量代换,即可得出答案.
19.(2 分)有一种用来画圆的工具板(如图所示),工具板长 21cm,上面依次排列着大小 不等的五
个圆孔,其中最大圆的直径为 3cm,其余圆的直径从左到右依次递减 0.2cm,最大圆的左侧工具板边
缘 1.5cm,最小圆的左侧距工具板右侧边缘 1.5cm,相邻两圆的间距 d 均相等,则相邻两圆的间距是
1.25 cm.
考点: 整数、小数复合应用题。522571
分析: 已知最大圆的直径为 3cm,其余圆的直径从左到右依次递减 0.2cm,先分别求出其它四个圆的
直径,用 21 厘米减去五个圆的直径,再减去左右两端的 1.5 厘米,又知道相邻两圆的间距 d
均相等,五个圆之间是四个间隔数,用所得的差除以 4 即可.由此列式解答.
解答: 解:其它四个圆的直径分别是;
3﹣0.2=2.8(厘米),
2.8﹣02=2.6(厘米),
2.6﹣0.2=2.4(厘米),
2.4﹣0.2=2.2(厘米),
五个圆的直径的和是:
3 2.8 2.6 2.4 2.2=13(厘米),
相邻两圆的间距是:
(21﹣13﹣1.5×2)÷4,
=(8﹣3)÷4,
=5÷4,
=1.25(厘米);
答:相邻两圆的间距是 1.25 厘米.
故答案为:1.25.
点评: 解答此题首先求出其它四个圆的直径,明确五个圆之间的间隔数是 4,用工具板的长度减去五
个圆的直径再减去左右两端的距离,然后用除法解答.
20.(2 分)一个质数如果加上 3 能被 2 整除,加上 2 能被 3 整除,在 40 以内符合条件的质数共有 5
个.
考点: 整除的性质及应用;合数与质数。522571
分析: 1 加上 3 能被 2 整除,加上 2 能被 3 整除,但 1 即不是质数,也不是合数;7 加上 3 得 10 能
被 2 整除,加上 2 得 9 能被 3 整除;13 加上 3 得 16 能被 2 整除,加上 2 得 15 能被 3 整除;
从 1 到 7,从 7 到 13,都是加 6,即 2 和 3 的最小公倍数,13 6=19,19 3=22,22÷2=11,19 2=21,
21÷3=7,所以 19 是质数也满足条件,19 6=25,25 不是质数;25 6=31,31 是质数,(31 3)
÷2=17,(31 2)÷3=11,满足条件;31 6=37,37 是质数,(37 3)÷2=20,(37 2)÷3=13 满
足条件;37 6=43 超出 40,因此得解.
解答: 解:(7 3)÷2=5,
(7 2)÷3=3;
7 6=13,13 6=19,19 6=25=5×5,不是质数,25 6=31.,(31 3)÷2=17,
(31 2)÷3=11,31 6=37,(37 3)÷2=20,(37 2)÷3=13;
答:个质数如果加上 3 能被 2 整除,加上 2 能被 3 整除,在 40 以内符合条件的质数共有 5 个,
分别是 7,13,19,31,37.
点评: 此题考查了整除的性质及应用,灵活应用合数和质数的性质来解决实际问题.
二、反复比较,慎重选择(每小题 2 分,共 10 分)
21.(2 分)下面图形是用木条钉成的支架,最不容易变形的时( )
A.
B.
C.
D.
考点: 三角形的特性。522571
分析: 根据三角形的特性:三角形具有稳定性;进行解答即可.
解答: 解:下面图形是用木条钉成的支架,最不容易变形的带有三角形的那个;
故选:B.
点评: 本题考查三角形稳定性的实际应用,三角形的稳定性在实际生活中有着广泛的应用.
22.(2 分)一个真分数,它的分子、分母同时加上一个相同的非零自然数后,所得到的新分数一定
( )
A. 与原数相等 B. 比原数大 C. 比原数小 D. 无法确定
考点: 分数大小的比较。522571
分析: 举例证明,的分子加上 1,分母加上 1 得到 ,> ,的分子加上 1,分母加上 1 得到 , ,
的分子加上 3,分母加上 3 得到 , > ,…据此解答
解答: 解:一个真分数,它的分子、分母同时加上一个相同的非零自然数后,所得到的新分数一定
比原数大;
故选 B.
点评: 本题主要考查利用由特殊到一般的推断方法
23.(2 分)随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费按原标准每分钟降低了 a 元
后,再次下调了 25%,现在的收费标准是每分钟 b 元,则原收费标准每分钟为( )元.
A. b﹣a B. b a C. b a D. b a
考点: 用字母表示数。522571
分析: 设原收费标准每分钟为 x 元,则根据题意,以现在的收费标准为等量关系,列出等式,表示
出原收费标准即可.
解答: 解:设原收费标准每分钟为 x 元,
由题意得,(x﹣a)(1﹣25%)=b,
(x﹣a)×75%=b,
x﹣ a=b,
x= b a.
故选:C.
点评: 解答本题的实质是实现从基本数量关系的语言表述到用字母表示一种转化,设出未知数,借
助方程,列出等式,从而求出答案.
24.(2 分)四个同样大小的圆柱拼成一个高为 40 厘米的大圆柱时,表面积减少了 72 平方厘米,原
来小圆柱的体积是( )立方厘米.
A. 120 B. 360 C. 480 D. 720
节省篇幅,其余详细解答及电子稿私信“小升初分班考试”,七个字,系统自动回复,多了或者少了系统都回复不到
,