基础准备
均值比较的假设检验是数据分析最重要的分析内容之一,根据参与比较的样本数量不同,使用的假设检验方法也不同,做个简要的总结:
一个总体均值与一个常数进行比较(Z检验和t检验);
两个总体均值之间的比较(Z检验和T检验);
三个及三个以上总体均值的比较(方差分析);
与Z检验和T检验不同,方差分析的结果只能检验出三个以上的总体均值是完全相同呢?还是不完全相同?注意是不完全相同,至于是哪个或哪些总体均值与其它总体均值不同则是不能获知的。因此方差分析结束以后还需要做事后多重检验,分析出到底是哪个或哪些总体均值与众不同。
今天我们要介绍的是进行事后多重检验的方法介绍。如果对方差分析还不太熟悉的朋友可以点击下面的链接回顾:
数据分析技术:方差分析原理;
数据分析理论:方差分析模型;
很多朋友会有疑问,为什么方差分析一定要进行事后多重比较呢?直接用独立样本T检验进行多次两两比较不是也可以吗?我们可以用一个例子说明这个原因:以方差分析为例,假如有5个样本,如果要进行多次均值的两两比较,那么两两比较的次数多达10次。设每次比较的显著性水平等于0.05,那么10次比较都不犯“弃真”错误的概率为(1-0.05)的十次方,也就是0.60左右,也就是说犯“弃真”错误的概率高达0.40,这远远大于原先设定的显著性水平0.05。不仅如此,随着比较组数的增多,犯“弃真”错误的概率也会越来越大。
SPSS的事后多重检验方法
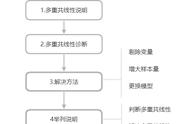
应用SPSS进行方差分析时,给分析者提供了很多事后多重检验的方法,如下图所示。这些方法根据多个总体方差是否相等分成了两大类。

事后多重检验的方法很多,但并不是说它们如百花齐放般的衬托了统计学的欣欣向荣,而是说明到目前为止仍然没有统一的解决方法,因此才根据不同的目的和数据情况创造出了很多不同的方法。
两两比较的方法
LSD法:最小显著性差异法(Least Significance Difference),是最简单的比较方法之一。它是t检验的一个简单变形,并未对检验水准做出任何校正,只是在标准误(注意不是标准差)的计算上充分考虑了所有总体水平的样本信息,估计出了一个更为稳健的标准误。因为单次比较的显著性水平a保持不变,所以LSD法是最灵敏的事后多重比较法。
Sidak法:Sidak校正在LSD法上的应用。通过Sidak校正降低每次两两比较的“弃真”错误概率,以使最终整个比较的“弃真”错误概率保持为显著性水平a。这也就是说每次比较的显著性水平a会随着比较次数的增多而减小。显然,Sidak法比LSD法的灵敏度低。每次进行Sidak比较的显著性水平为:

Bonferroni法:与Sidak法类似,它的每一次比较实际上是Bonferroni校正在LSD法上的应用。Bonferroni法修正后每次比较的显著性水平比Sidak法的更小,也就是说Bonferroni法比Sidak法的灵敏度更低。

Scheffe法:Scheffe法的实质是对多个总体均值间的线性组合是否为0进行假设检验。多用在两组样本含量不同的情况。
Dunnett法:常用于多个试验组与一个对照组间的比较。因此在指定Dunnett法时,还应当指定对照组。
以上五种方法的排列顺序是按照灵敏度从高到低排列的,LSD法>Sidak法>Bonferroni法>Scheffe法>Dunnett法。
形成同质亚组的方法
SNK法:全称为Student-Newman-Keuls法。它实质上是根据预先指定的准则将各组均值分为多个亚组,利用Studentized Range分布来进行假设检验,并根据所要检验的均值个数调整总的“弃真”错误概率不超过设定的显著性水平a。
Tukey法:全称为Tukey' s Honestly Significant Difference法。应用这种方法要求各组样本含量相同。它也是利用Studentized Range分布来进行各组均数间的比较,与SNK法不同地是,它控制所有比较中最大的“弃真”错误概率不超过设定的显著性水平a。
Duncan法:其思路与SNK法相类似,只不过检验统计量服从的是Duncan' s Multiple Range分布。
以上8种是常用的事后多重检验方法(各水平样本的方差齐性),剩下的六种方法并不常用,这里就不在介绍。除此之外,在各组样本方差不齐时,SPSS还提供了4种事后多重检验的方法,但从方法的接受程度和结果的稳健性讲,希望大家尽量不要在方差不齐时进行方差分析甚至两两比较,采用变量变换或者非参数检验往往更可靠。