要点归纳
1.解决圆周运动临界问题的一般思路
(1)要考虑达到临界条件时物体所处的状态。
(2)分析该状态下物体的受力特点。
(3)结合圆周运动知识,列出相应的动力学方程分析求解。
2.圆周运动与摩擦力有关的临界问题
(1)物体间恰好不发生相对滑动的临界条件是物体间恰好达到最大静摩擦力,此时静摩擦力提供向心力,则静摩擦力的方向指向圆心,大小为f=mv²/r。
(2)如果除摩擦力外还有其他力,此时的临界条件是静摩擦力达到最大且静摩擦力的方向分别为沿半径背离圆心或沿半径指向圆心。
与摩擦力有关的临界问题都是静摩擦力达到最大值。
3.圆周运动与弹力有关的临界问题
(1)在有压力、支持力的运动中,临界条件是物体间的弹力恰好为0。
(2)在有绳上拉力的运动中,临界条件是绳恰好拉直且无弹力或绳上拉力恰好为最大承受力等。
4.几种常见的临界情况
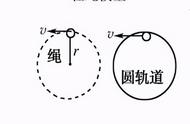
(1)竖直平面内圆周运动的临界问题,物体在竖直面内做的圆周运动是一种典型的变速曲线运动,该类运动常有临界问题,并伴有“最大”“最小”“刚好”等词语。根据运动至轨道最高点时的受力情况,可分为三种模型:一是只有拉(压)力,如球与绳连接,沿内轨道的“过山车”等,称为“轻绳模型”;二是只有推(支撑)力的,如汽车过拱形桥等,称为“拱桥模型”;三是可拉(压)可推(支撑),如球与杆连接、小球在弯管内运动等,称为“轻杆模型”。
(2)圆锥摆动态变化中的临界状态
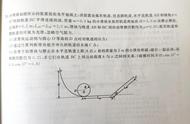
例题:如图所示,

在水平桌面上有一个固定竖直转轴且过圆心的转盘,转盘半径为r,边缘绕有一条足够长的细轻绳,细绳末端系住一木块。已知木块与桌面之间的动摩擦因数μ=√3/3。当转盘以角速度=√5rad/s旋转时,木块被带动一起旋转,达到稳定状态后,二者角速度相同。已知r=1m,下列说法正确的是()
A当=√5rad/s稳定时,木块做圆周运动的半径为2m
B.当=√5rad/s稳定时,木块的线速度与圆盘边缘线速度大小之比为4:1
C.要保持上述的稳定状态,角速度ω<√10√3/3rad/s
D.无论角速度多大,都可以保持上述稳定状态
例题:如图所示,

水平杆固定在竖直杆上,两者互相垂直,水平杆上O、A两点连接有两轻绳,两绳的另一端都系在质量为m的小球上,OA=OB=AB。现通过转动竖直杆,使水平杆在水平面内做匀速圆周运动,三角形OAB始终在竖直平面内,若转动过程OB、AB两绳始终处于拉直状态,则下列说法正确的是(BC)
A.OB绳的拉力范围为0~√3mg/3
B.OB绳的拉力范围为√3mg/3~2√3mg/3
C.AB绳的拉力范围为0~√3mg/3
D.AB绳的拉力范围为0~2√3mg/3
例题:如图,

轻杆长2l,中点装在水平轴O上,两端分别固定着小球A和B(均可视为质点),A球质量为m,B球质量为2m,重力加速度为g,两者一起在竖直平面内绕O轴做圆周运动
(1)若A球在最高点时,杆的A端恰好不受力,求此时B球的速度大小
(2)若B球到最高点时的速度等于第(1)问中的速度,求此时O轴的受力大小和方向
3)在杆的转速逐渐变化的过程中,能否出现O轴不受力的情况?若不能,请说明理由;若能,求出此时AB球的速度大小.
例题:如图所示,