学物理经常听说模型,到底是什么模型、模型这个概念有多重要、怎么利用模型?可以说,你现在接触的所有物理知识,都是建立在模型的基础上的。所以,研究物理学,建立模型是一个基础。那什么是建立模型呢?就是在处理某个实际问题的时候,把目标的变化用数学关系描绘出来,这就是建立模型了。在这个过程中,有三个核心问题:目标、变化、关系。本系列专题我们就从模型的角度来总结高考物理的解题方法。

疫情严重,作为一名教师,虽不能冲上一线,但也愿尽自己微薄之力。各地大中小幼院校,推迟开学,从今天起本人专栏免费(由于不能改成0元,故定价0.01)提供给各位学子,直至疫情结束!并愿意为大家提供免费答疑,私信即可,有问必回!各位学子加油!武汉加油!
模型11:竖直平面圆周运动模型的三个核心:
目标:解决竖直平面圆周运动
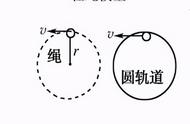
变化:球—绳模型或单轨道模型、球—杆模型或双轨道模型
关系:向心力的来源以及向心力与速度的关系
- 竖直平面圆周运动的临界极值问题
1.竖直面内圆周运动两类模型
一是无支撑(如球与绳连接、沿内轨道运动的过山车等),称为“轻绳模型”,二是有支撑(如球与杆连接、在弯管内的运动等),称为“轻杆模型”.
2.竖直平面内圆周运动的两种模型特点及求解方法

- 几个易错点和重要的二级结论
(1)不脱离轨道(比如内轨模型中,小球仅在下半圆运动,但也没有离开轨道)≠完整的圆周运动;
(2)超失重问题:上半圆失重、下半圆超重;
(3)光滑的内轨或绳球模型,最高点是临界速度,则最低点的速度是根号下5gR(动能定理)。

(4)小球从圆心等高处自由下落,在光滑轨道内做圆周运动,则最低点对轨道的压力为3mg,与R无关(动能定理)。