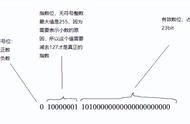
如4个位的补码方案可以表示的数据范围:

10.3 原码和补码的优缺点分析
原码表示法:
优点:与日常使用的十进制表示方法一致,简单直观。
缺点:加法与减法运算规则不统一,增加了成本;整数0 有“00000000”和“10000000”两种表示形式,不方便。
补码表示法:
优点:加法与减法运算规则统一, 没有“-0”,可表示的数比原码多一个(-2n-1)。
缺点:不直观,人使用不方便。
10.4 原码和补码可表示的整数范围
原码可表示的整数范围:
8位原码: - 27 1~27- 1(- 127~127)
16位原码: - 215 1~215- 1(- 32767~32767)
n 位原码: - 2n-1 1~2n-1- 1
补码可表示的整数范围:
8位补码:- 27~27- 1 (- 128~127 )
n位补码:- 2n-1~2n-1- 1
- 128表示为 10000000
127 表示为 01111111
10.5 整数在计算机中的表示的对比
计算机中整数有多种,同一个二进制代码表示不同类型的整数时,其含义(数值)可能不同。
一个代码它到底代表哪种整数(或其它东西),是由指令决定的。

10.6 实数的特点与表示方法
实数是既有整数部分又有小数部分,小数点位置不固定。
任何一个实数总可以表达成一个乘幂和一个纯小数之积。
例如:
56.725 = 0.56725×10^2
-0.0034756 = -0.34756×10^-2
实数的表示方法(记阶法/浮点表示法):用3个部分表示:
乘幂中的指数(也称阶码):表示实数中小数点的位置。
纯小数部分(尾数):表示实数中的有效数字部分。
数的正负(符号)。
二进制实数的浮点表示:
与十进制实数一样,二进制实数也可以用记阶法表示,如:
1001.011B = 0.1001011B×2^ 100
-0.0010101B = -0.10101B×2^-10
可见,任一个二进制实数 N 均可表示为:
N=±S×2P
(其中, ±是该数的符号; S是N 的尾数;P是N的阶码)
因此,32位的单精度浮点数在计算机中可表示为:
由于指数(阶码)可以选用不同的编码(原码、补码等),尾数的格式和小数点位置也可以有不同的规定,因此早期计算机中浮点数的表示方法互不相同。
现代计算机中,一般都以IEEE 754标准存储浮点数,这个标准的在内存中存储的形式为:
对于不同长度的浮点数,阶码与小数位分配的数量不一样,如对于32位的单精度浮点数,数符分配是1位,阶码分配了8位,尾数分配了是23位:

符号位:0表示正;1表示负;
偏移阶码e:e=指数的实际值 127。
假有一个浮点数10110010.001,则指数是7,阶码就要用7 127的二进制数表示,也就是:111 01111111 = 10000110
尾数使用原码表示,绝对值在1与2之间,其中1和小数点都是隐含的,并不直接表示。