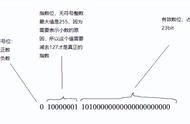
根据这个标准,我们来尝试把一个十进制的浮点数转换为IEEE754标准表示。
例如:178.125
先把浮点数分别把整数部分和小数部分转换成2进制:
整数部分用除2取余的方法,求得:10110010
小数部分用乘2取整的方法,求得:001
合起来即是:10110010.001
转换成二进制的浮点数,即把小数点移动到整数位只有1,即为:1.0110010001 * 2^111,111是二进制,由于左移了7位,所以是111
把浮点数转换二进制后,这里基本已经可以得出对应3部分的值了:
数符:由于浮点数是正数,故为0(负数为1)。
阶码 : 阶码的计算公式:阶数 偏移量, 阶码是需要作移码运算,在转换出来的二进制数里,阶数是111(十进制为7),对于单精度的浮点数,偏移值为01111111(127)[偏移量的计算是:2^(e-1)-1, e为阶码的位数,即为8,因此偏移值是127],即:111 01111111 = 10000110
尾数:小数点后面的数,即0110010001
最终根据位置填到对位的位置上:

可能有个疑问:小数点前面的1去哪里了?由于尾数部分是规格化表示的,最高位总是“1”,所以这是直接隐藏掉,同时也节省了1个位出来存储小数,提高精度。
浮点数的二进制显示可以使用以下代码:
#include<iostream> #include <bitset> //STL的bitset模板类 using namespace std; void main() { union { float input; int output; } data; data.input = 178.125; std::bitset<sizeof(float) * 8>bits2(data.output); //bitset模板类定义对象,<>内为长度,()为值 //如bitset<8> bitset2(12); //长度为8,二进制保存,前面用0补充 std::cout << bits2 << std::endl; system("pause"); } //01000011001100100010000000000000
-End-