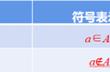
一、判断元素与集合关系的两种方法
I(1)直接法:如果集合中的元素是直接给出的,只要判断该元素在已知集合中是否出现即可,此时应先明确集合是由哪些元素构成的。
(2)推理法:对于某些不便直接表示的集合,只要判断该元素是否满足集合中元素所具有的特征即可,此时应先明确已知集合的元素具有什么特征,即该集合中元素要满足哪些条件。
二、已知元素与集合的关系求参数的思路
当a属于A时,若集合A是用描述法表示的,则a一定满足集合中元素的共同特征,如满足方程(组)不等式(组)等;若集合A是用列举法表示的,则a一定等于集合A中的某个元素。反之,当a不属于A时,结论恰恰相反,利用上述结论建立方程(组)或不等式(组)求解参数即可,注意根据集合中元素的互异性对求得的参数进行检验。

三、已知集合相等求参数的方法
要寻找两个集合中元素之间的关系,需通过列方程或方程组求解。当集合中未知元素不止一个时,要分类与整合,求出参数值后要注意检验是否满足集合中元素的互异性。

四、集合的表示方法的选取原则
要根据集合元素所具有的属性选择适当的表示方法。列举法的特点是能清楚地展现集合的元素,通常用于表示元素个数较少的集合,当集合中元素较多或无限时,就不宜采用列举法;描述法的特点是形式简单、应用方便,通常用于表示元素具有明显共同特征的集合,当元素共同特征不易寻找或元素的限制条件较多时,就不宜采用描述法。
五、集合与方程的综合问题的解题思路
(1)弄清方程与集合的关系,用集合表示方程的解集,集合中的元素就是方程的根。
(2)当方程中含有参数时,若方程是一元二次方程,则应综合应用一元二次方程的相关知识求解,若知道其解集,利用根与系数的关系,可快速求出参数的值(或参数之间的关系);若知道解集中元素个数,利用判别式可求参数的取值范围。
,