在上面的讲义中,关于区间的概念已做了一点解释。在这次的讲义中又做重点提示,因为这个知识点的名词术语比较多,应用的标记符号也比较多,容易记混。同时也要求同学们要把区间这个知识点重视起来,真正学好,学透。为以后深入学习有关内容,做好基础知识的储备。
一,区间的概念与应用
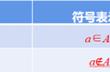
设α、b∈R,且α<b
1、闭区间的定义
{x丨α≤ⅹ≤b},符号是[α,b]
2、开区间的定义
{x|α﹤x﹤b},符号是(α,b)
3、半开半闭区间定义
{x|α≤x<b},符号是[α,b)
4、半闭半开区间定义
{x|α<x≤b},符号是(α,b]
(说明,半开半闭区间和半闭半开区间,这两个名称也可以用一个名称来表达,即、"半开半闭区间"。现行《教参》的版本不同,有的名称也不同,还是要以现行的教材为准。)
5、无穷区间的定义
{x丨x≥α},符号是[α, ∞)
{ⅹ丨x>α},符号是(α, ∞]
{ⅹ丨ⅹ≤b},符号是(-∞,b]
{x丨ⅹ﹤b,符号是(-∞,b)
关于区间的概念与应用在数轴是怎样表示的,希望同学们认真研读教材中的图形与标记符号。
同学们在研读教材教参时,一定要结合教材教参的讲解部分,进行深入的研究和细致的分析。注意,区间是实数集的又一种表达形式,要考虑到以下四种情况
1、区间的左端点必须小于右端点,有时我们将b一α称为区间的长度。对于只有一个元素的集合,我们仍然用集合来表示,例如.{α}
2、注意开区间(α,b)与点(α,b)与具体情况和环境中的区别
3、用数轴表示区间时,要特别注意实心点与空心点的区别
4、对于一个不等式的解集,我们可以用集合的形式来表示,也可以用区间的形式来表示。
再就是,在研读和深入理解区间的概念时,要特别注意以下四点(一)、区间符号里面的两个字母或数字之间一定要用","隔开
(二)、区间实际就是用一类特殊的数集(部分实数组成的集合)的符号表示
(三)、区间表示实数集的三个基本准则。
(1)、是连续的数集;
(2)、左端点必须小于右端点;
(3)、开或闭不能混淆、
(四)、注意"∞"是一个趋向符号,表示无限的接近,却永远不能到达。不是一个数,因此以"-∞"和" ∞"为区间的一端时,这个端点必须用小括号。
关于区间的概念与应用,以及区间是实数集的又一种表达形式,我就重点的给同学们提示这些。我们在研读教材的具体内容时,一定要反复阅读教参的中的有关重点提醒,当然我的提示也是反复阅读教材和教参的一些相关的内容,给同学们做的重点提示。
希望同学们能够把我的这个重点提示,结合教材和教参进行认真的研读,以便我们把区间这个知识点更好的学深学透,为以后进一步学习有关方面的知识,打下一个良好的基础。
(注、我在写这个讲义稿时,有的地方引用教材和教参的原文。也有的语句是我自己的话,有错误的地方,希望读者和编审官提出来,以免误导学生,谢谢!)
,