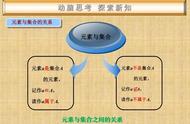
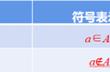
主要内容:
本文主要介绍几组不等式在不同情形求解的主要步骤。着重需要注意的是函数的定义域、值域的理解和函数乘积不等式解集的求解方法。
根据不等式特征,对于A=x^2 x 1,其判别式有:
△=1^2-4*1<0,所以二次抛物线A=x^2 x 1与x轴没有交点,
则x^2 x 1>0,
此时原不等式的解集与不等式x 1>0同解,故:
x≥-1,综上可得该不等式的解集为:
{x| x≥-1,x∈R}。

本不等式中有平方项,即(2x 1)^2≥0,
需要注意的是取等号的情况,所以:
原不等式的解集等同于:
1x 52<0,且x≠-1/2,
则x≤-1/52且x≠-1/2,
此时不等式解集为:
{x| x≤-1/52且x≠-1/2, x∈R}。

该不等式中含有对数,二次幂,在解不等式的同时还需要考虑对数的定义要求,即对log2x要有意义,则x为正数。此时不等式分两种情况进行讨论。
(1)当log2x-2<0且x^2-4>0时,即:
log2x<log2(2^2)且x^2>4,则:
x<4且x>2或者x<-2,考虑x为非负数,
所以不等式的解集写成区间为:(2,4)。
(2)当log2x-2>0且x^2-4<0时,即:
log2x>log 2(2^2),则x>4,此时不满足后一个不等式,故此时无解。
综上所求不等式的解集为:(2,4)。

该不等式前者为自然对数,且e^x-1=0的零点是x=0,
后者是一元二次方程80x^2-42x 1=0,可以进行因式分解,有两个零点,
所以方程(e^x-1)(80x^2-42x 1)=0有三个零点,然后再根据解不等式零点穿插法,即可得到不等式的解集。
先对后者因式分解有:
80x^2-42x 1=0.
(2x-1)(40x-1)=0,
即两个零点为x1=1/2,x2=1/40。
根据三个零点的大小关系,此时可写成所求不等式的解集为: