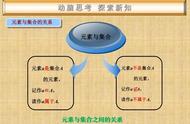
集合贯穿高中数学的整个过程,是学习其他知识点的基础,也是数学核心素养抽象思维的要求,集合的概念与表示要掌握集合的概念,集合的性质,表示方法,学会用符号语言表示集合,了解空集的含义。
一、集合的概念
一般地,我们把指定的某些对象的全体称为集合.通常用大写英文字母A,B,C,…表示.
集合中的每个对象叫作这个集合的元素,通常用小写英文字母a,b,c,…表示.
1.集合的概念同平面几何中的点、线、平面等类似,只是描述性的说明.
2.集合是一个整体,暗含“所有”“全部”“全体”的含义.一些对象一旦组成了集合,这个集合就是这些对象的总体.
3.组成集合的对象可以是数、点、图形、符号等,也可以是人或物等.
二、元素与集合的关系
1.a∈A与a∉A取决于元素a是否在集合A中,这两种情况中必有且只有一种成立.
2.符号“∈”“∉”只能用在元素与集合之间,表示元素与集合之间的从属关系.具有方向性.

三、集合中元素的三个特性
1.确定性的作用是判断一组对象能否组成集合.
2.互异性的作用是警示我们做题后要检验.特别是题中含有参数(字母)时,一定要检验求出的参数是否使集合的元素满足互异性.
3.无序性的作用是方便定义集合相等,当两个集合相等时,其元素一定相同,但不一定依次对应相等.

四、几种常用的数集及其记法

常用数集之间的关系