五、集合的表示方法
1.列举法
列举法是把集合中的元素一一列举出来写在花括号“{ }”内表示集合的方法,一般可将集合表示为
用列举法表示集合时,必须注意以下几点:
(1)元素与元素之间必须用“,”隔开;
(2)集合的元素必须是明确的;
(3)不必考虑元素出现的先后顺序;
(4)集合的元素不能重复;
(5)集合的元素可以表示任何事物;
(6)对含有较多元素的集合,如果该集合的元素具有明显的规律,可用列举法表示,但是必须把元素间的规律显示清楚后,才能用省略号表示,如N 也可表示为.
2.描述法
描述法是通过描述元素满足的条件表示集合的方法.
一般可将集合表示为{x及x的范围|x满足的条件},即在花括号内先写出集合中元素的一般符号及范围,再画一条竖线“|”,在竖线后写出集合中元素所具有的共同特征.
(1)用描述法表示集合应写清楚该集合中的代表元素,即代表元素是数、有序实数对、集合,还是其他形式.
(2)准确说明集合中元素的共同特征.
(3)所有描述的内容都要写在集合符号内,并且不能出现未被说明的字母.但是,如果从上下文的关系看,代表元素的范围明确,可以省略.如非常明确x∈R,则“∈R”可以省略.
(4)用于描述的语句力求简明、准确,多层描述时,要准确使用“且”“或”等表示描述语句之间关系的词
六、集合的分类
1.集合可以根据它含有的元素的个数分为两类:
含有有限个元素的集合叫作有限集,含有无限个元素的集合叫作无限集.
2.把不含有任何元素的集合叫作空集,记作⌀.
(1)集合的分类是按照集合中元素是有限个还是无限个划分的,不是按元素多少,一个集合中元素有很多,但是个数有限,也属于有限集.
(2)空集中不含有任何元素,{0}不是空集,因为它含有元素0.
空集是有限集还是无限集? 空集可以看成包含0个元素的集合,所以空集是有限集.
七、区间及其表示
1.设a,b是两个实数,且a<b我们作出规定:

这里的实数称为区间的端点.[a,b]称为闭区间,(a,b)称为开区间 ,[a,b),(a,b]称为 半闭半开区间.
在数轴上表示区间时,用实心点表示属于区间的端点,用空心点表示不属于区间的端点.
2.数集R也可用区间表示为(-∞, ∞),“∞”读作“无穷大”,“-∞”读作“负无穷大”,“ ∞”读作“正无穷大”.还可把满足x≥a,x>a,x≤b,x<b的实数x的集合分别表示为如下情况

1.区间左端点的值小于右端点的值.
2.有完整的区间外围记号.
3.区间符号中的两个端点(字母或数字)之间只能用“,”隔开
一般地,确认一组对象均不相同)能否构成集合的过程为:

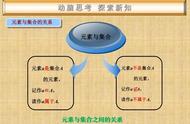
判断元素与集合的关系的两种方法
(1)直接法:如果元素是直接给出的,那么只要判断该元素在已知集合中是否出现即可.此时应明确集合是由哪些元素组成的.
(2)推理法:对于一些元素没有直接给出的集合,只要判断该元素是否满足集合中元素所具有的特征即可.此时应明确已知集合中的元素具有什么特征.
根据集合中元素的确定性解出字母参数的所有可能取值,再根据集合中元素的互异性进行检验.互异性是元素的三个特性中最常用的一个,解答含有字母参数的元素与集合之间关系的问题时,要具有分类讨论的意识.
①解决集合相等的问题易产生与互异性相矛盾的情况,所以解题后需要进行检验和修正.
②有些数学问题需要根据题目的要求和特点分成若干类,转化成若干个小问题来解决,这种按不同情况分类,然后再逐一研究解决问题的数学方法就是分类讨论的方法.
1.使用列举法表示集合时,应注意以下几点:
(1)在元素个数较少或元素间有明显规律时可用列举法表示集合.
(2)“{}”表示“所有”的含义,不能省略,元素之间无顺序,满足无序性.
2.用列举法表示集合,要分清该集合是数集还是点集.
用描述法表示集合需要注意的有:
1.用描述法表示集合时应弄清楚集合的属性,即它是数集、点集还是其他的类型.一般地,数集用一个字母代表其元素,点集用一个有序实数对代表其元素.
2.若描述部分出现代表元素以外的字母,则要说明新字母含义或指出其取值范围.
表示集合时,应先根据题意确定符合条件的元素,再根据元素情况选择适当的表示方法.
值得注意的是,并不是每一个集合都可以用两种方法表示出来.