什么叫做小概率不发生原理（怎么理解小概率事件不会发生） - 原点资讯

1. 卫生统计学：是应用概率论和数理统计学的基本原理和方法，研究居民卫生状况以及卫生服务领域中数据的收集、整理和分析的一门科学。

2. 同质(homogeneity)：在统计学中，若某些观察对象具有相同的特征或属性称为同质的。否则称为异质(heterogeneity)的或者间杂的。

3. 变异(variation)：同质事物之间的差别称为变异。[没有个体变异，就没有统计学！]

4. 总体(population)：根据研究目的所确定的同质观察单位的全体。

5. 样本(sample)：是从总体中随机抽取的具有代表性的部分观察单位的集合。

6. 样本含量(sample size)：样本中包含的观察单位个数。

7. 参数(parameter)：反映总体特征的指标。特点：未知、唯一，希腊字母表示，如总体均数、总体率等。

8. 统计量(statistic)：根据样本观察值计算出来的指标。特点：已知、不唯一，拉丁字母表示，如样本均数、样本率等。

9. 变量(variable)：研究者需要对每个观察单位的某项特征或属性进行观察或测量，这种特征或属性称为变量。

10. 变量值(value of variable)：变量的观察值或测量值称为变量值或观察值(observed value)。

11. 资料(data)：变量值的集合称之为资料。

12. 定量资料(quantitative data)：变量值是定量的，表现为数值大小。特点：一般有度、量、衡单位，一般属连续性资料。

13. 定性资料(qualitative data)：观察值是定性的，表现为互不相容的类别或属性。特点：一般无度、量、衡单位，一般属于离散型资料。可进一步分为计数资料和等级资料。

14. 计数资料(count data)：将观察单位按某种类别或属性进行分组，清点各组观察单位数所得的资料。可进一步分为二项分类资料和无序多项分类资料。

15. 等级资料(ordinal data)：将观察单位按照某种特质或属性的程度或等级顺序分组，清点各组观察单位所得的资料。各属性之间互不相容且有程度的差别。

16. 抽样研究(sampling research)：从总体中随机抽取样本，通过样本信息推断总体特征的研究方法。

17. 抽样误差(sampling error)：由随机抽样造成的样本统计量与总体参数之间、样本统计量之间的差异。

18. 概率(probability)：概率是随机事件发生可能性大小的数值度量。通常用P表示。大小介于0与1之间，即0≤P ≤1。

19. 小概率事件：医学研究中，将概率小于等于0.05或0.01的事件称为小概率事件。

20. 小概率原理：并不表示不可能发生，但在某一次试验中，是不会发生的。

21. 单纯随机抽样(simple random sampling)：先将调查总体的全部观察单位统一编号，然后采用随机数字表、统计软件或抽签等方法之一随机抽取n（样本大小）个编号，由这n个编号所对应的n个观察单位构成研究样本。

22. 系统抽样(systematic sampling)：又称机械抽样或等距抽样。事先将总体内全部观察单位按某一顺序号等距分隔成n（样本大小）个部分，每一部分内含m个观察单位；然后从第一部分开始，从中随机抽出第i号观察单位，依此用相等间隔m机械地在第2部分、第3部分直至第n部分内各抽出一个观察单位组成样本。

23. 分层抽样(stratified sampling)：是先按对观察指标影响较大的某项或某几项特征，将总体分成若干层，该特征的测定值在层内变异较小、层间变异较大，然后分别从每一层内随机抽取一定数量的观察单位结合起来组成样本。

24. 整群抽样(cluster sampling)：是将总体划分为群（初级观察单位），各群由次级观察单位组成。随机抽取一部分群，调查抽中群的全部次级观察单位。

25. 信度(reliability)：测量工具的可靠性，它是指采用相同测量工具（如问卷）对同一对象进行重复测量时，各次测量值与其均值接近的程度。

26. 效度(validity)：是指测量工具、指标或观测结果在多大程度上反映了事物的客观真实性，即指观测结果与试图达到的目标之间的接近程度，是对测量工具（如问卷）有效性的检验。

27. 实验研究(experimental study)：是指研究者根据研究目的人为地对受试对象（包括人或动物）施加处理因素，控制混杂因素，观察、总结处理因素的效应的一种研究方法。

28. 处理因素(study factor，treatment)：是指研究者施加于受试对象的因素。

29. 水平(level)：是指同一处理因素在数量上或强度上的不同程度。

30. 受试对象(study subjects)：是处理因素作用的客体或对象。

31. 实验效应(effect)：是处理因素作用于受试对象后出现的反应和结局，它通过指标的选择和指标的观察来体现。

32. 偏倚(bias)：研究误差中的系统误差部分称为偏倚。

33. 平均数(average)：表达了一组同质定量数据的平均水平或集中位置。常用的平均数包括算术均数、几何均数、中位数、众数、调和均数等。

34. 算术均数(mean)：常简称均数，是用一组观察值相加除以观察值的个数所得。常用x(__)表示样本均数，表示μ总体均数。

35. 几何均数(geometric mean)：用G表示，是n个观察值乘积的n次方根，又称倍数均数。适用于：①对数对称分布，②等比级数资料，如血抗体浓度。[观察之中不能有0]

36. 中位数(median)：用M表示，是将一组观察值由小到大排序后，居于中间位置的数值即为中位数。中位数是一种位置平均数。

37. 百分位数(percentile)：用表示，是指将一组观察值由小到大排序后，将其平均分成100等份，对应于每一分割位置上的数值就称为一个百分位数。

38. 医学参考值范围：亦称正常值范围，是指绝大多数“正常人”的解剖、生理、生化等指标的波动范围。

39. 率(rate)：是说明某现象发生的频率或强度的指标，不会大于1。

40. 构成比(proportion)：表示事物内部各组成部分所占的比重，常以百分数表示，因此也称为百分比。

41. 相对比(ratio)：是两个指标A、B之比。A、B可以是绝对数，A、B也可以是相对数，A、B可以是性质相同的两个指标，A、B的单位可以相同，也可以不同。

42. 动态数列(dynamic series)：是一系列按时间顺序排列起来的统计指标，用以说明事物在时间上的变化和发展趋势。

43. 率的标准化：是在一个指定的标准构成条件下进行率的对比的方法。意义：当两个率要进行比较大小时，若要对比的两组对象内部构成的差别足以影响结论时，可以应用率的标准化法消除这种影响，使两个率具备可比性。

44. 标准误(standard error，SE)：通常将样本统计量的标准差称为标准误。

45. 可信区间(confidence interval，CI)：按一定的概率或可信度(1-a)用一个区间估计总体参数所在范围，这个范围称作可信度为1- a 的可信区间，又称置信区间。

46. Poisson分布：Poisson分布是二项分布的极限形式，二项分布中，当π很小（<0.05），n很大，二项分布→Poisson 分布。

47. Ⅰ型错误(type Ⅰ error)：H0实际上是成立的，但由于抽样的原因，拒绝了H0，这类“弃真”的错误称为Ⅰ型错误，其最大概率为α。

48. Ⅱ型错误(type Ⅱ error)：H0实际上不成立，但假设检验没有拒绝它，这类“取伪”的错误称为Ⅱ型错误，其概率大小用β表示。

49. 检验效能(power of a test)：1-β，是指当两总体参数确有差别时，按α水准能够发现这种差别的能力。即对实际上成立的H1作出肯定结论的把握程度。

50. P值：指从所规定的总体中随机抽样，获得等于或大于现有统计量值的概率。

51. 参数检验(parametric test)：在总体分布类型已知的条件下，在此基础上对未知的参数进行估计或检验，称为参数统计或参数检验。

52. 非参数检验(nonparametric test)：不依赖于总体的分布类型，不对总体参数进行推断，只是通过样本观察值比较总体的分布或分布位置，因此又称为任意分布检验。

53. 直线相关(linear correlation)：又称简单相关(simple correlation)，是用来描述具有直线关系的两变量x、y的相互关系的统计方法。

54. 直线相关系数(linear correlation coefficient)：亦称Pearson积矩相关系数，是定量描述两个变量间直线关系的方向和密切程度的指标。总体相关系数用ρ表示，样本相关系数用r表示。

55. 死亡事件(death event)：又称失效事件/重点事件，指标志某种处理措施失败或失效的特征事件。

56. 生存时间(survival time)：指观察到的存活时间，可用天、周、月、年等时间单位记录，常用符号t表示。

57. 完全数据(complete data)：从观察起点至发生死亡事件所经历的时间。

58. 结尾数据(censored data)：简称结尾值，又称删失数据或终检值。生存时间观察过程的截止不是由于死亡事件，而是由于其他原因因引起的，称为结尾。主要原因有三种：失访、退出、终止。

59. 生存曲线(survival curve)：以观察（随访）时间为横轴，以生存率为纵，将各个时间点所对应的生存率连接在一起的曲线图，用以描述生存过程。

60. 寿命表(life table)：是根据特定人群的年龄组死亡率编制出的一种统计表，用以说明在特定人群年龄组死亡率的条件下人的生命过程。

1. 卫生统计学的主要内容：

⑴统计设计；⑵统计分析；⑶生命统计；⑷常用统计分析软件简介。

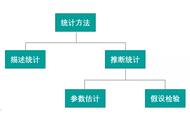
2. 统计分析包括：

⑴ 统计描述：定量资料和定性资料的统计描述，统计表和统计图。

⑵ 统计推断：主要包括参数估计和假设检验。

3. 统计工作的基本步骤：⑴设计；⑵收集资料；⑶整理资料；⑷分析资料。

4. 参数VS统计量：参数是反应总体特征的指标；统计量是样本指标。

5. 资料类型：

⑴ 定量资料

⑵ 定性资料：①计数资料；②等级资料。

6. 产生抽样误差的根源：个体差异

7. 医学研究方法主要有：⑴调查研究；⑵实验研究；⑶文献研究。

8. 常用抽样方法：⑴单纯随机抽样；⑵系统抽样；⑶分层抽样；⑷整群抽样。

9. 抽样误差从小到大：分层抽样<系统抽样<单纯随机抽样<整群抽样

10. 实验设计的基本原则：

⑴对照原则；⑵随机原则；⑶重复原则；⑷均衡原则。

11. 常用的实验设计方案：⑴完全随机设计；⑵配对设计；⑶随机区组设计；⑷交叉设计；⑸析因设计；⑹重复测量设计。

12. 实验设计的三要素：⑴处理因素；⑵受试对象；⑶实验效应。

13. 中位数适用于：偏态分布资料、一端或两端无确切数据的资料、总体分布不明资料的资料。

14. 描述离散趋势常用的变异程度指标：极差、四分位数间距、方差、标准差、变异系数。

15. 正态分布的参数：⑴均数μ；⑵标准差σ。

① μ是位置参数，σ一定时，μ越大，曲线越向右移动；

σ是形状参数，μ一定时，σ越大，曲线越平阔。

② 标准正态分布：μ=0，σ=1。

16. 标准差VS标准误：

⑴ 标准差表示个体差异的大小，描述资料的频数分布状况，可用于制定医学参考值范围。

⑵ 标准误描述样本均数的变异程度，说明抽样误差的大小，用于总体均数的区间估计和假设检验。

17. 用正态近似法进行总体率的区间估计的条件：

⑴ n足够大；

⑵ p和1-p均不太小；

⑶ np和n(1-p)均大于5。

18. Poisson分布特点：方差与均数相同。

19. 产生抽样误差的原因：⑴抽样误差；⑵个体变异(本质差别)

20. x2检验校正后的变化：x2值偏小，P值偏大。

21. 等级资料进行统计比较时：用秩和检验或Ridit分析。

22. 老资料满足参数检验，却选用非参数检验的结果：降低检验效能，增大犯Ⅱ型错误的概率。

23. 生存曲线的特点：

为一条下降的曲线。平缓表示生存率高或较长生存期，陡峭表示生存率低或较短生存期。

24. 比较贡献大小采用：标准化的偏回归系数。

25. 样本含量估计：

⑴ 接近0.5

⑵ 若要求相同的检验标准，两组例数相等时所需样本含量较少。

⑶ α可以取双侧，也可以取单侧；β只能取单侧。

26. 影响检验效能的要素：

⑴样本含量；⑵客观事物差异的大小；⑶个体间变异的大小；⑷α值。

27. 如何增大检验效能：

⑴增大α；⑵增加样本含量。

【正态分布的特征】

1. 正态曲线在横轴上方均数处最高，向两侧逐渐下降，并以均数为中心，左右对称，但两端与横轴永不相交，呈钟形曲线。

2. 正态分布有两个参数，即均数和标准差。μ是位置参数，σ一定时，μ越大，曲线越向右移动；σ是形状参数，μ一定时，σ越大，曲线越平阔。

3. 正态曲线下面积的分布有一定的规律：正态分布曲线下一定区间内的面积代表了取值于相应区间内的观察值个数在全部观察值总数中所占的比例（频率），或者是观察值落在该区间内的概率：

① 正态曲线与横轴之间的面积恒等于1或100%；

② 正态分布为对称分布，其对称轴两侧的面积各为50％；

③ 区间(μ-σ，μ σ)面积为68.27%；

区间(μ-1.96σ，μ 1.96σ)面积为95%；

区间(μ-2.58σ，μ 2.58σ)面积为99%。

【制定医学参考值的原则、常用方法和适用条件】

1. 原则：①要确定一批样本含量足够大的“正常人”；②根据研究目的和使用要求选定适当的百分界值，如80%，90%，95%和99%，常用95%；③根据专业知识确定单侧或双侧界值；④根据资料的分布特点，选用恰当的计算方法。

2. 常用方法和适用条件：

① 正态分布法：适用于正态或近似正态分布的资料

双侧界值：

单侧上界：单侧下界：

② 百分位数法：常用于偏态分布资料以及资料中一端或两端无确切数值的资料

双侧95%参考值范围为：P2.5～P97.5

单侧上界为：P95或单侧下界为：P5

【Ⅰ型错误VSⅡ型错误】

1. 重点减少Ⅰ型错误：α可取小，如0.01；重点减少Ⅱ型错误：α可取大，如0.2。

2. α越大，Ⅱ型错误越小，检验效能1-β越大。

3. P≤α拒绝H0时，只犯Ⅰ型错误；P>α不拒绝H0时，只犯Ⅱ型错误。

4. 双侧检验P≤α，单侧必得P≤α；单侧检验P＞α，双侧必得P＞α。

5. 单侧检验易犯Ⅰ型错误，双侧检验易犯Ⅱ型错误，单侧效能高于双侧。

【假设检验】

前提条件

①总体具有同质性；②样本具有代表性和组间可比性。

基本步骤

①建立检验假设，确定检验水准；

②选定检验方法和计算检验统计量；

③确定P值，做出推断结论。

注意事项

1. 应有严密的研究设计：

①总体中的每个研究个体应具有同质性；②样本资料应具有代表性；③比较的组间应具有可比性。

2. 正确理解α水准和P值的意义

3. 正确理解结论的统计学意义

4. 假设检验的结论不能绝对化

【t检验】

含义	一种以t分布为基础，以t值为检验统计量的计量资料的假设检验方法。
基本思想	假设在H0成立的条件下做随机抽样，按照t分布的规律获得现有样本检验统计量t值的概率为P，将P值与事先设定检验水准α进行比较，判断是否拒绝H0
应用条件	①独立性；②正态性(可用正态性检验来确认)；③方差齐性(可由方差齐性检验来认定)。
主要用途	①单个样本均数与总体均数的比较； ②配对设计资料的差值均数与总体均数的比较； ③成组设计的两样本均数差异的比较。

【方差分析】

含义	一种以数据分析的变异为基础，以F值为统计量的计量资料的假设检验方法。
基本思想	将全部观察值之间的总变异按设计类型分解为两个或多个组成部分，通过比较不同变异来源的均方，借助F分布做出统计推断。
应用条件	①独立性；②正态性(可用正态性检验来确认)；③方差齐性(可由方差齐性检验来认定)。
主要用途	多个样本均数的比较(三个及三个以上)

【x2检验】

含义	一种以x2分布为基础，以x2值为检验统计量的计数资料的假设检验方法。
基本思想	通过x2值的大小反映实际频数(A)和理论频数(T)的符合程度，在H0成立时，实际频数(A)和理论频数(T)的相差不应该很大，果实际频数(A)和理论频数(T)的相差很大，则H0成立的可能性很小。
应用条件	①独立性；②正态性(可用正态性检验来确认)；③方差齐性(可由方差齐性检验来认定)。
主要用途	①推断两个或两个以上总体率(或构成比)之间有无差别； ②两变量间有无相互关系；③检验频数分布的拟合优度。
2×2表的x2检验的注意事项	①当n≥40且所有T≥5时，用2×2表x2检验的基本公式或专用公式计算x2值； ②当n≥40但有1≤T＜5时，需要用校正公式计算x2值； ③当n＜40或有T＜1时，不宜计算x2值，需采用Fisher确切概率法直接计算概率。
R×C表的x2检验的注意事项	①允许有不超过1/5的基本格子理论频数大于1小于5，但不能有理论频数小于1； ②如果有1/5以上格子的理论频数大于1小于5，或有1个格子的理论频数小于1，可增加样本含量。

【非参数检验的优、缺点】

优点：①适用于任何分布的资料；

②不受总体方差一致的限制；

③可用于等级资料的统计分析；

④有些问题本身没有适当的参数检验方法而非参数检验则恰能处理。

缺点：①由于它没有充分利用原始数据中所提供的信息故检验效能低；

②其效果有一定近似性。

【秩和检验】

含义	亦称符号秩和检验或Wilcoxon配对法，属于非参数检验(不依赖于总体分布类型，不对总体参数进行推断，只是通过样本观察值推断总体的分布或分布位置是否有差别)。
基本思想	在H0成立的前提下，差值(配对差值、样本各测量值和已知总体中位数M0的差值)的总体分布是对称的，总体中位数应为0，T 与T-应接近n(n 1)/4。若正负秩和相差悬殊，则有理由怀疑H0的成立。
适用条件	①不满足参数检验条件的资料及无法经变量变换满足参数检验条件的资料； ②未加精确测量的资料，如一端或两端为不确定数值的资料； ③分布类型未知的资料。
主要用途	①推断配对设计资料差值的总体中位数是否为0； ②推断样本所来自总体的中位数与已知总体中位数是否相等。

【等级相关适用范围】

1. 不服从双变量正态分布的资料；

2. 总体分布类型未知的资料； 3. 等级资料。

【直线回归分析】

含义	直线回归是研究两个连续性变量间线性依存关系的一种统计分析方法，用直线回归方程描述两个变量间变化的数量关系，属双变量分析的范畴。
前提条件	①独立性；②正态性(可用正态性检验来确认)；③方差齐性(可由方差齐性检验来认定)。
应用条件	①两变量的变化趋势呈直线趋势； ②因变量y为来自正态分布的随机变量，x可以是规律变化的或人为选定的一些数值(I型回归)，也可以是随机变量(II型回归)； ③对于I型回归，当x取不同数值时，y的分布都是正态分布，并且这些分布的方差都相等；对于II型回归，要求x、y服从双变量正态分布。
注意事项	①作回归分析要有实际意义； ②直线回归分析的资料，一般要求应变量y是来自正态总体的随机变量； ③进行回归分析时，应先绘制散点图； ④异常值的处理(通过散点图判断)； ⑤避免外延。

【直线回归与直线相关分析区别与联系】

VS		直线相关	直线回归
区别	资料要求不同	要求两个变量是双变量正态分布。	要求应变量y服从正态分布，自变量x是能精确测量或控制的变量。
	统计意义不同	反映两变量间的伴随关系，这种关系是相互的，对等的，以一定有因果关系。	反应变量之间的依存关系，有自变量和应变量之分，一般将“因”或交易测定、变异较小者定为自变量，这种依存关系可能是因果关系或从属关系。
	分析目的不同	把两变量间直线关系的密切程度及方向用一个统计指标表示出来。	把自变量与应变量间的关系用函数公式定量地表达出来。
联系	变量间关系的方向一致：对同一资料，其r与b的正负号一致。
	假设检验等价：对同一样本，tr=tb
	r与b值可相互换算(书上找)
	用回归解释相关：回归分析中的决定系数在数值上等于相关系数的平方，即r2。