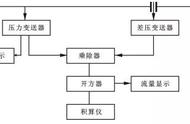
已知此曲线在最低点的曲率半径为该点到x轴距离的2倍,重力加速度为g。
求: (1)小球运动到任意位置P(x,y)的速率v。
(2)小球在运动过程中第一次下降的最大距离ym
(3)当在上述磁场中加一竖直向上场强为E,E>(mg/q)的匀强电场时,小球从O点静止释放后获得的最大速率vm.
【解析】应用动量定理求第(3)问,竖直距离最大,竖直速度为零,重力向下,对水平方向动量无贡献,在水平方向应用动量定理。
qBVy·t=m·△Vx
qBy=mv
洛伦兹力不做功,(qE-mg)y=mv²/2
得:y=mv/qB
(qE-mg)mv/qB=mv²/2
v=2(qE-mg)/qB

例题:如图甲所示,空间存在一范围足够大的垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.让质量为m、电荷量为q(q>0)的粒子从坐标原点O沿xOy平面以不同的初速度大小和方向入射到该磁场中,不计重力和粒子间的影响。
(1)若粒子以初速度v₁沿y轴正向入射,恰好能经过x轴上的A(a,0)点,求v₁的大小;
(2)已知一粒子的初速度大小为v(v>v₁),为使该粒子能经过A(a,0)点,其入射角θ(粒子初速度与x轴正向的夹角)有几个?求出对应的sinθ值;
(3)如图乙所示,若在此空间再加入沿y轴正向、大小为E的匀强电场,一粒子从O点以初速度v₀沿y轴正向发射研究表明:粒子在xOy平面内做周期性运动,且在任一时刻,粒子速度的分量vx,与其所在位置的y坐标成正比,比例系数与电场强度大小E无关求该粒子运动过程中的最大速度值vm。

【解析】第(3)问,洛伦兹力不做功,速度最大,电场力不再做功,即速度与电场力垂直。
电场力在竖直方向,在水平方向上不影响动量。

在水平方向上应用动量定理:qBVy·t=mVx=mVm
qBy=mVm
mVm²/2-mv₀²/2=qEy(动能定理)
可求Vm。