反比例函数上的四个点,能不能围成一个正方形?我们首先需要了解反比例函数的图像与性质。反比例函数的图像是双曲线,当k>0时,反比例函数过第一、三象限;当k<0时,反比例函数过第二、四象限。并且,反比例函数的图像关于原点成中心对称性,关于直线y=x或y=-x成轴对称。由于反比例函数的定义域x≠0,那么反比例函数与y轴没有交点;反比例函数定义中k≠0,那么反比例函数与x轴也没有交点。即反比例函数的图像无限地接近x轴、y轴,与x轴、y轴没有交点。

了解清楚反比例的图像与性质后,我们再看问题,四个点围成的四边形为正方形,那么正方形有什么特点呢?要证明一个四边形为正方形,我们可以先证明其为平行四边形。

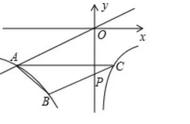
过点O任意地作直线AC与双曲线交于点A、点C,过点O任意地作直线BD与双曲线交于点B、点C,那么直线AC与直线BD是正比例函数,正比例函数也关于原点成中心对称。由对称性可知,点A与点C关于原点成中心对称,点B与点D关于原点成中心对称,那么OA=OC,OB=OD,由此我们可以证明四边形ABCD为平行四边形。

那么,怎么由平行四边形变成正方形呢?我们可以先证明平行四边形为菱形,再证明菱形的对角线相等或一个内角为直角从而得到正方形;或者先证明平行四边形为矩形,再加上邻边相等或者对角线互相垂直从而得到正方形。当满足OA=OB=OC=OD,即对角线互相平分且相等时,该四边形为矩形,但是可以发现该四边形的对角线不可能互相垂直。互相垂直的两条直线的比例系数K的乘积互为负倒数,而直线AC与直线BD都过第一、三象限,比例系数K都是正数,乘积不可能等于-1。

由此可知,反比例函数上任意四点围成的四边形,可以是平行四边形,也可以是矩形,但是不能为菱形,也不能为正方形。
,