知识点:反比例函数面积问题、同底等高三角形面积、同底三角形面积比、相似三角形面积比。
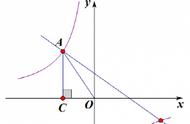
如图,已知双曲线y=12/x(x<0),和y=k/x(x>0),直线OA与双曲线y=12/x交于点A,将直线OA向下平移与双曲线y=12/x交于点B,与y轴交于点P,与双曲线y=k/x交于点C,S△ABC=6,BP:CP=2:1,求k。

分析:因为BC是由OA平移得到,所以BC∥OA,连接OB、OC,所以S△OBC=S△ABC=6(同底等高)
作BE⊥y轴于点D,CF⊥y轴于点F

易证:△BEP~△CFP
∴BE/CF=BP/CP=2:1
∴S△BEP:S△CFP=4:1①
S△BPO:S△CPO=2:1(同底三角形面积比等于高的比)
∴S△BPO=2/3.S△OBC=4
S△CPO=1/3.S△OBC=2
∵反比例函数y=12/x
∴S△BEO=6
∴S△BEP=S△BEO−S△BPO=6−4=2
由①得:S△CFP=1/2
∴S△CFO=S△CPO−S△CFP=2−1/2=3/2
∵k<0
∴k=−3。
,