以函数为载体的平行四边形存在性问题是近年来中考的热点,其图形复杂,知识覆盖面广,综合性较强,对学生分析问题和解决问题的能力要求高.考生往往因为选择方法不得当而导致计算量偏大,或因分类情况不完整而导致漏解。各类平台期刊杂志对这类问题求解文章不少,但我这里老调新弹,旗帜鲜明在理论提出新体会型策略,期待对这类难题易于切入操作,学生易于突破。
对这类题,常规解法是先画出平行四边形,再依据"平行四边形的一组对边平行且相等"或"平行四边形的对角线互相平分"来解决.由于先要画出草图,若考虑不周,画图有两种方法,一是作平行线,二是倍长中线,特别要注意的是,无论是哪一种类型,如果没有明确四边形顶点的顺序,则需要分类讨论。处理这类问题的策略是数形结合,先形后数即先画图,再利用方程解决!

预备知识:解题切入点

类型1 两定点两动点形成的平行四边形存在性问题
策略:平行找相等线段法:可以利用一组对边平行且相等的四边形是平行四边形,这时候需要用到两点之间的距离公式(可以利用勾股定理计算),因为已知的两点所在的直线解析式可以求出,再利用平行线的k值相等,设平行于已知直线的解析式为y=kx b,分别联立方程求出两个交点的坐标(用含有b的式子表示),再计算这两个交点之间的距离,使这个距离等于已知两点之间的距离。

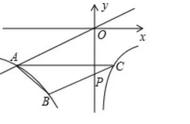
例1.(2018秋•武昌区期中)如图,抛物线y=ax*2 bx﹣3与x轴交于A,B两点(A点在B点左侧),A(﹣1,0),B(3,0),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
(1)求抛物线的函数解析式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.