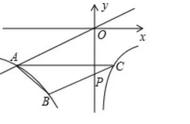
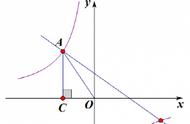
总结:这种题型,关键是合理有序分类:无论是三定一动,还是两定两动,统统把抛物线上的动点作为第四个动点,其余三个作为定点,分别以这三个定点构成的三条线段为对角线分类,分三种情况讨论,然后运用平行四边形顶点坐标公式转化为方程(组).这种解法,不必画出平行四边形草图,只要合理分类,有序组合,从对角线入手不会漏解,条理清楚,而且适用范围广.其本质是用代数的方法解决几何问题,体现的是分类讨论思想、数形结合的思想.此类题目主要考查平行四边形的判定与性质、函数解析式的确定与性质,考查识图作图、运算求解、数学表达等能力,数形结合、分类讨论、函数与方程等数学思想。学生在处理问题的时候,往往不能正确分类,导致漏解。
巧用对角线探究平行四边形的适度拓展:在一些问题中,还常常会要求学生讨论菱形、矩形的存在性。此时我们可在上述基础上增加相应条件,如增加两条对角线互相垂直、邻边相等得到菱形,增加邻边互相垂直、对角线相等得到矩形,利用点坐标求得相应线段的长度从而求解。事实上利用坐标求解的思路还适用于等腰三角形、直角三角形、圆的存在性问题。有时,我们甚至还可以通过构造平面直角坐标系来求解。