九上:和最小与差最大问题
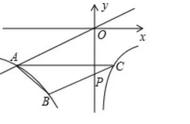
原 题 再 现 | 如图所示,一次函数y=mx n (m≠0)的图象与反比例函数y=k/x (k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过点A作x轴的垂线,垂足为C,△AOC的面积为4. (1)分别求出a和b的值; (2)结合图象直接写出mx n>k/x中x的取值范围; (3)在y轴上取点P,当PB-PA取得最大值时,求出点P的坐标.
|
考 察 知 识 | 本题是反比例函数的待定系数法,两个函数值大小比较通法,差最大问题。 |
解 题 思 路 |
|
参 考 答 案 | 第(3)问解题思路分析:
解:(1)反比例函数的表达式为 y= -8/x 解得a=4,b=8. (2)解集为x<-2或0<x<8. (3)点P(0,17/3) |