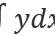01 引言
数学上一种重要的方法是由简单到复杂的学习方法。也就是简化运算过程,着重致力于方法的学习。下面以直角坐标系下二重积分计算为例进行说明。
02 直角坐标系下二重积分计算方法的学习思路
1 因为二重积分的计算过程较为复杂,尤其是被积函数为多项式的二重积分的计算,涉及到二元函数求偏导的反运算,使得计算过程较为复杂。
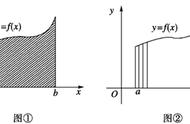
2 为了简化运算过程,着重致力于方法的学习。不妨用大学方法做小学、初中的题。比如求平面中三角形的面积或被积函数为常数的二重积分的计算。由简单问题的做题过程可以总结出二重积分的计算方法为,先将积分微元变为dx.dy。然后结合题意,用中学的知识画图,由图形一般可看成左右边界固定的x型域,或者上下边界固定的y形域。由积分区域写出x和y的取值范围,谁的取值范围固定,先写谁的积分,写成两次定积分,先做后边的积分,求得的结果前移,形成定积分,从而求出结果。采用这样的方法,结合x型或y型域,可得到求二重积分的一题两解法。
采用同样的方法,再应用于被积函数为单项式的二重积分的计算,除了要分离变量外,可以采用与被积函数为常数的二重积分类似的方法。
采用上述类似的方法再做被积函数为多项式的二重积分方法仍然不变。只是在做后面积分时,应采用二元函数求偏导数的反运算求出被积函数的原函数。将原函数的上限值减下限值所求得的结果前移,形成定积分,从而求出结果。
03 结论
综上所述,本文介绍了由简单到复杂的学习方法在直角坐标系下二重积分的计算上的应用。这样的方法,可以简化运算过程,突出方法原理的学习。从而在数学学习上带来半功倍的效果。
,