用比例解决问题:
首先我们知道比例分:正比例和反比例
概念:
1、正比例:两种相关联的量的比值一定,这两种量成正比例关系。
举例:(以水费、用水量、水的单价为例)
每吨水的单价(价钱)是一个固定的数,那么水的单价、用水量和水费的关系则是:
水费:用水量=水的单价(固定、不变)
当水的单价固定不变时,水费增加时,用水量也会随着增加;水费减少时,用水量也会随着减少。
2、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中对应的两个数的乘积一定,这两种量就叫做反比例的量,它们的关系叫做反比例关系。
举例:单位时间内的用电量*用电时间=总用电量(固定、不变)
当总用电量不变时,单位时间内的用电量增加,那么用电时间就会减少;如果单位 时间内的用电量减少,那么用电时间就会增加。
我们来对比下正比例与反比例的异同点:
相同点:正比例与反比例都有两种相关联的量
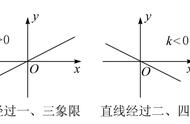
不同点:正比例:“变化方向”相同,一种量增大或减少,另一种量也同时增大或减少。
相对应的两个量的比值(商)一定,关系式是Y/X=K
反比例:“变化方向”相反,一种时增大或减小,另一种量反而减少或增大。
相对应的两个量的积一定,关系式X*Y=K

解题思路:
1、首先先找出两种相关联的量;
2、判断它们是否是正比例或反比例关系;
3、根据正比例的意义列出方程;
4、解方程
注意:无论应用正比例,还是应用反比例,解决问题时,要先弄清是相关联量的积不变,还是商不变,都体现了变中有不变的思想。
,