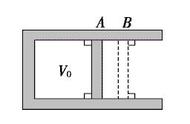
由上图所示:
Sx=S∆AOC Sy=S∆AOB Sz=S∆BOC Sn=S∆ABC (式2)
设ɑ是∆ABC与平面xOz的夹角,则∆AOB是∆ABC在平面xOz的投影,从而:
S∆AOB=S∆ABCcosɑ(式3)
这个四面体可以看做是整个流体的一部分。
显然,只有当这个四面体的体积足够小,是一个微元的时候,才能看做一个深度的质点,否则它本身有高度的话,那么就和题意要求的“某一深处”的条件矛盾了。
假设液体整体处于静止状态,那么这个四面体作为液体的一部分,根据上面的“流体基本性质2”可知,四面体也处于静止状态。
现在对该四面体进行受力分析:

除了它在四个面分别收到的压力之外,它还受到重力作用,其大小G=Mg
(其中M代表四面体的质量,g是重力加速度常量)
设液体的密度为ρ,则M=ρV,其中V是四面体体积。
V是受力面积与高的乘积,高与两个面的夹角相关,所以可以看出:
由于四面体是微元,所以受力面积趋向0、V是相对于受力面积的高阶无穷小。
从而可以推出:
推论1:G是相对于相对于Fz的高阶无穷小,忽略不计。
由上图:
在y轴方向上,合力应为0,所以:
Fy=Fncosɑ (式4)
将式1代入式4,得到:
PySy=PnSncosɑ (式5)
将式2代入式5,得到:
PyS∆AOB=PnS∆ABCcosɑ (式6)
将式3代入式6,得到:
Py=Pn
同理可证Px=Pn
结合推论1,也可证得Pz=Pn
从而有:Px=Py=Pz=Pn,命题得证。
总结数学是一切自然科学的基础,大部分物理学结论其实都是根据思想实验 数学推导,得到大致方向性结论,然后再辅以实验进行验证。而并不是像很多人所想的那样——物理规律的发现完全来自没有方法与策略支撑的实验。


往期原创科普文章回顾:
别忘了点击文末广告,作为对作者原创的打赏和支持哦:),感谢!
,