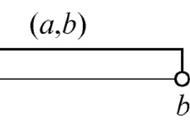一致连续性是高数一个比较难理解的概念,特别是在开区间上的一致连续性,更令人难以把握。因为根据一致连续性定理,闭区间上的连续函数自然就一致连续,但开区间就没有这样的定理。那么包括开区间在内的有限区间上,一致连续性到底还需要什么必要条件呢?

这个必要条件就是有界性。因为连续函数在闭区间上具有有界性定理,所以闭区间上的连续函数一定一致连续,但开区间上的连续函数就未必有界,所以开区间上的连续函数就不一定具有一致连续性。下面我们一起来证明一下函数在有限区间上一致连续的这个必要条件。
设I为有限区间. 证明:若f在I上一致连续,则f在I上有界,举例说明此结论当I为无限区间时不一定成立.
所谓必要条件,就是由一致连续的结论可以推出的条件。包括连续性和有界性,都是函数在有限区间上一致连续的必要条件。但这里只探究有界性。
证:设区间I的左右端点为a,b. ∵f在I上一致连续,【因为I没有确定为开区间还是闭区间,所以不写成(a,b)或[a,b]的形式】
∴对ε0=1,存在正数δ<(b-a)/2,当|x’-x”|<δ(x’,x”∈I)时,有|f(x’)-f(x”)|<1.【这是一致连续性的定义的应用,定义中的ε是任取的,但有时候,我们只需要取其中一个ε0就可以了,ε0的值可以任取,但我们会取需要的数,而δ取得比I的长度的一半小,可以避免下面所取邻域之间的互相干扰】
令a1=a δ/2, b1=b-δ/2,则a<a1<b1<b.【从这里开始,把I分成三个部分来探究,中间是一个闭区间[a1,b1],取两个端点与原端点的距离正好等于δ/2,就有两则的区间正好符合ε0=1的一致连续性定义不等式,上面的它的长度大于I的长度的一半,两边的两个区间各有一个端点可闭可开】
∵f在[a1,b1]上连续,∴f在[a1,b1]上有界,设|f(x)|≤M1, x∈[a1,b1].【连续函数在闭区间上的有界性定理的应用】
当x∈[a,a1)∩I时,∵0<a1-x<δ/2, ∴|f(x)-f(a1)|<1,【[a1,b1]左侧的半闭开区间[a,a1)与I的交集中的任意点x,就都在a1的左邻域U-(a1,δ/2)上,满足前面所取的ε0=1的一致连续性定义不等式】
有|f(x)|<|f(a1)| 1. 【这就证明f在[a,a1)上有界,自然在(a,a1)上也是有界的】
同理当x∈(b1,b]∩I时,有|f(x)|<|f(b1)| 1. 【即f(x)在I的三个部分上都有界】
令M=max{M1,|f(a1)| 1,|f(b1)| 1},则对一切x∈I,必有|f(x)|≤M. 即f在有限区间I上有界.【取三个部分的界的最大值,就是b函数在整个I上的界。】
例证:y=x, x∈R一致连续,但lim(x→ ∞)x= ∞无界.

现在你对一致连续性有更深的认识了吗?
,