―、错误理解溶解度与都只受温度彩响
例1 —定温度下,已知氣化银的Ksp(AgCl) =1.8 ×10-10,取过量的氯化银溶于水制成的20 mL 溶液向里面加 入20 mL 0.1 mol/L的NaCl,求该温度下此溶液中氯化银溶解度为多少?
错误解析:认为物质的溶解度在一定温度下是定值,直接把Ksp(AgCl) =1.8 ×10-10 。开平方得c(Ag+)为 1.34 × 10-5,结合体积算出AgCl的质量.
正确解析:溶解度不只和温度有关,还受溶剂的种类、 是否与溶剂反应以及其中有无同离子情况有关。因为有Cl-这种同离子使得AgCl此时溶解度减小,因此计算得c(Cl-)为 20 ×0. 1/(20 +20)mol/L,再由 Ksp(AgCl)=c(Ag+) ×c(Cl-)去算出c(Ag+)为 3.6×10-9 mol/L,再由c(Ag+)结合体积去求算AgCl的质量•
例2下列叙述不正确的是( )
A. CaCO3能够溶解在CO2的水溶液中
B.Mg(OH)2可溶于盐酸,不溶于NH4C1溶液
C. AgCl可溶于氨水
D. MgSO4溶液中滴加Ba(OH)2只得到一种沉淀
A、C两项考虑与溶剂发生反应溶解容易排除;而B项 要考虑到Mg(OH)2溶解平衡受到NH4+消耗OH-而得到促进:所以答案选BD.
例3向含有AgCl(s)的饱和AgCl溶液中加水,下列叙 述正确的是( )
A. AgCl的溶解度增大
B. AgCl的溶解度、Ksp均不变
C. Ksp(AgCl)增大
D. AgCl的溶解度、Ksp均增大
只要知道Ksp只受温度的影响不难选出B。
小结溶解度和温度、溶剂的种类、性质、是否有新反应以及其中有无同离子等情况有关,而为溶度积与普通化 学平衡常数类似只受温度的影响.
二、错误理解难溶物溶解平衡达到后,溶液中离子浓度与图像的关系
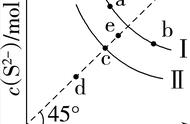
例 4 常温下,ksp( CaSO4) = 9 × 10 -6 ,常温下 CaSO4 在 水中的沉淀溶解平衡曲线如图1。下列说法正确的是( )

A.常温下CaSO4饱和溶液中c(Ca2+)、c(SO42-)对应曲 线上任意一点
B. b点将有沉淀生成,平衡后溶液c(SO42-)一定等于 3 ×10-3 mol/L
C.d点溶液通过蒸发可以变到c点
D.a点对应的等于C点对应的Ksp
答案选D。最易误选A项或B项,A项认为达到溶解平衡后溶液饱和了就是表示各离子溶度为曲线上的任意值,其实应c( Ca2+ )、c(SO42-)的乘积对应曲线上任意一点;B项,b点时Qc>Ksp, 将有沉淀生成,Ca2+、SO42-的浓度按相同 数值减小,通过计算得平衡后溶液c(SO42-)小于 3 ×10-3 mol/L。
三、错误理解难溶物的溶解度与其Ksp变化一致
典型例证:BaSO4和Mg(OH)2两物质,溶解度BaSO4为 2.4 × 10-4 g,Mg( OH)2 为 9 ×10-4 g,Mg( OH)2比 BaSO4的 溶解度大,溶度积Ksp ( BaSO4 ) = 1. 1 × 10-10,而 Ksp[Mg(OH)2] =1.8×10-11,Mg(OH)2的溶度积小,结合表达式就知道这与物质平衡关系式中各离子的浓度和系数都有联系的。对同类型的难溶电解质(阴阳离子数目比相同的),如AgCl, AgBr, AgI, BaSO4等,在相同温度下,Ksp越 大,溶解度就越大,Ksp越小,溶解度就越小。对于不同类型的 (阴阳离子数目比不相同的)如BaSO4和Mg( OH)2,溶度积小的,溶解度不一定小。
四、错误理解沉淀转化
很多学生从AgNO3溶液依次加入氯化钠溶液、溴化钠 溶液、碘化钾等溶液中都会出现不同颜色的沉淀,得出溶解度小的沉淀可以转化成溶解度更小的沉淀后乱用结论。
如有入认为在有Cl-和Br-共同存在的溶液中,只要 滴入AgNO3溶液,就必定先有AgBr沉淀生成! ”这种结论错在机械运用巳有规律,没有考虑Cl-和Br-的浓度。因为这 要看原溶液c(Cl-)、 c(Br-)的大小,因为形成沉淀必须 满足的条件c(Ag+)× c(X-)>Ksp(AgX),如c(Cl-)较 大,而c(Br-)较小,c(Ag+) × c( Cl-)>Ksp(AgCl),而c(Ag+) ×c(Br-)<ksp(AgBr)时,则先生成 AgCl 沉淀。
又如有入认为:同类型的电解质BaSO4与BaCO3溶解度是BaCO3较大,那么可以在BaCO3中加入Na2SO4使 BaCO3变成BaSO4;但是BaSO4加不可能转化成 BaCO3。这种错误的理解是忽略了沉淀转化也是溶解平衡的移动造成的这个因素。既然是平衡那么就有向正、逆两个方 向移动的可能,其实沉淀转化的规律应该是:沉淀容易从溶解度大的转化成溶解度更小的,反之困难,不一定不可以。如 BaSO4用饱和Na2CO3洗可转化成BaCO3,当然用稀Na2CO3 达不到要求.
五、常见几种涉及计算的正误辨析
例5 巳知 AgCl(s)

Ag+ + Cl-,
Ag2CrO4(s)

2Ag+ + CrO42-,
且Ksp(AgCl)=c(Ag+)× c(Cl- ) =1.8 ×10-10, Ksp(Ag2CrO4) =[c(Ag+)]2 •c(CrO42-)=1.9×10-12,现用 0.01 mol/L AgNO3溶液滴定 0. 01 mol/L KC1 和 0.001 mol /L K2CrO4混合溶液,通过计算完成下列问题:
(1) Cl-、CrO42-谁先沉淀?
(2) 当刚出现Ag2CrO4沉淀时,溶液中Cl-浓度是多少? (设混合溶液在反应中体积不变)
常见问题:解析第一个问时,有不少学生会不考虑Cl-、 CrO42-两浓度而直接比较Ksp(AgCl)与Ksp(Ag2CrO4)得出 Ag2CrO4先沉淀。
这里他们犯的错误主要是忽视了AgCl、Ag2CrO4是不同类型的电解质,他们溶解度和ksp不一致,而且Cl-、CrO42-两离子浓度也不同,这时就必须利用进行计算后看对于Cl-、CrO42-离子哪个需要AgNO3的体积比较小就能达到其 就是那个先沉淀!
正确解析设混合溶液为1 L,沉淀Cl-需AgNO3溶液体积为x L,沉淀CrO42-需AgNO3溶液为y L.则
(0.01 mol / L × x ) × (0. 01 mol /L ×1) = 1. 8 × 10-10 × x= 1.8 ×10-6 L
(0.01 mol /L ×y)2 × (0.001 mol /L ×1) =1.9×10-12,y=4.36×10-3 L
因为x<y,所以Cl-先沉淀.
解析第二个问题时,常有入认为因AgCl先沉淀就会形成AgCl饱和溶液得出c(Ag+)•c(Cl-)=1.8×10-10因为 是AgCl饱和溶液,c( Ag+) =c(Cl- )对1 .8 × 10-10开平方 就得到答案了。
这里错误主要以为住何难容电解质的饱和溶液中阴阳离子比和化学式的比例一样为定值;但是这不是单一溶质的 水溶液,CrO42-的存在会影响c( Ag+),只能这样算:
因c(Ag+)]2 ×c(CrO42-)=1.9×10-12,[ c(Ag+)]2 × 0.01 mol /L =1.9×10-12,c(Ag+) =4.36×10-5 mol • L-1,c(Ag+) ×c(Cl-)=1. 8 × 10-10,4. 36 ×10-5 ×c(Cl-)=1.8×10-10 ,c(Cl-) =4.13 × 10-6 mol /L.
例6巳知25℃,电离常数Ka(HF) =3.6×10-4,溶度积常数ksp(CaF2) =1.46×10-10 ,现向1L 0.2 mol/L HF 溶液中加入1 L 0. 2 mol • L-1 CaCl2溶液,下列说法正确的是 ( )
A. 25 ℃ 时,0.1 mol • L-1 HF 溶液的 pH = 1
B. Ksp( CaF2)随温度和家度的变化而变化
C. 该体系中Ksp(CaF2) =1/Ka(HF)
D.该体系中有CaF2沉淀生成
本题选D.。B、C两项很容易排除,而A、D项主要考査运用近似计算。因Ka( HF) = 3. 6 ×10-4 ,结合离子方程式c (H+) ×c(F- )÷c(HF) =3.6×10-4,[c(H+)]2÷[0.1 -c(H+)] =3.6×10-4,这里要把[0.1-c(H+)]近似看成 0.1进行计算会发现A项不对;对于D项要注意本题是混合溶 液不要错认为HF和CaCl2还都是0. 2 mol /L,应该都是 0.1 mol/L。结合A项的近似计算法可求c(H+)=c(F-) =6×10-2 c(Ca2+)× [c(F-)]2>Ksp(CaF2)。
注意:溶解平衡中常用到近似计算,但要注意有选择性 ,不然会出现错误的近似结果。
,