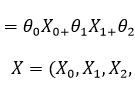这里的m是样本的数量,是一个常数,我们对均方差乘上这个系数并不会影响 θ 的取值。这个 J(θ) 就是我们常说的模型的损失函数,这里它代表的意义是所有样本均方差的平均数的1/2。
这里的损失其实是误差的意思,损失函数的值越小,说明模型的误差越小,和真实结果越接近。
我们计算J(θ)对θ的导数:

我们令导数等于0,由于m是常数,可以消掉,得到:

上面的推导过程初看可能觉得复杂,但实际上并不困难。只是一个简单的求偏导的推导,我们就可以写出最优的θ的取值。
从这个公式来看并不难计算,实际上是否真的是这么简单呢?我们试着用代码来实验一下。
代码实验
为了简单起见,我们针对最简单的场景:样本只有一个特征,我们首先先试着自己生产一批数据:

我们先生成一百个0~2范围内的x,然后y= 3x 4,为了模拟真实存在误差的场景,我们再对y加上一个0~1范围内的误差。
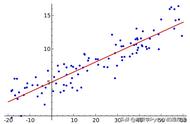
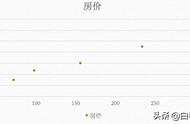
我们把上面的点通过plt画出来可以得到这样一张图: