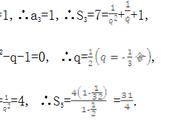初探
大一的学生上高数的时候,往往会被老师告知,当s<=1的时候,∑1/n^s是发散的,这个结论在s为实数域是没错的,但是一旦把s的范围解析延拓到复数域,那么除了s=1以外,s在整个复数域都是收敛的。也就是说,全体自然数之和在s解析延拓后是收敛的,那么究竟等于多少呢?黎曼告诉我们——全体自然数之和=-1/12!!!(纳尼),许多同学或许感觉不可思议,的确,这个式子违背了我们的直觉,正数之和为什么会等于负数呢?下面小编就用最简单的方法证明一下为什么全体自然数之和等于-1/12。

我们重点来看一下最后推出的方程

重要的解析延拓方程
我们把s=2代入上面的式子,由于ζ(s)=∑1/n^s,因此∑n=2(2π)^-2*1!*cosπ*∑1/n^2,我们知道cosπ=-1,∑1/n^2=π^2/6,因此求得∑n=-1/12,也就是全体自然数之和等于-1/12!是不是很神奇呀。但是好奇心比较重的小伙伴可能会问,还有什么发散级数解析延拓后能够求和吗?答案是大部分发散级数在解析延拓后都能够求和。
拓展关于发散级数求和主要有两种方法:zeta和borel求和,我重点来讲一下zeta求和,因为简单直观,下面我先给出zeta求和最重要的两个公式:

非交错级数求和