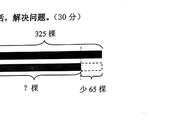
《三位数除以一位数(商是两位数)》教学设计
【教学内容】
青岛版三年级上册第六单元信息窗二《三位数除以一位数(商是
两位数)》
【教学目标】
1.通过动手操作、自我尝试等方式引领学生理解三位数除以一位
数的算理,在理解算理的基础上,掌握正确的计算方法。
2.引导学生利用已有知识进行类推,探索三位数除以一位数的笔 算方法;同时明白三位数除以一位数有的商是三位数,有的商是两位
数。
3.引导学生认真观察、动脑思考,在与他人交流算法的过程中获
得成功的体验;
【教学重难点】
教学重点:理解算理,掌握方法。
教学难点:商首位的书写位置。
【教学具准备】
多媒体课件、三角板
【教学过程】
一 、回顾旧知,导入新课
师:同学们,在第一单元我们已经学习过《三位数除以一位数》
---看这两道题,你会算吗?谁来说一下答案。(生交流)
ppt 出示: 480÷2 248÷2
我们一起回顾一下248÷ 2这道题是怎样计算的?----课件演
示
师:同学们这个数字2,它会变,瞪大眼睛仔细看,2变成了什
么?
【设计意图:学习是基于学生原有知识经验基础上的自我建构, 学生头脑中的知识结构组织得越好,就越利于保存和应用。简单的复 习,既能马上集中学生的注意力,又能唤醒学生已有的知识储备。正 所谓温故而知新,相信数形结合展示计算过程, 一定会为学生主动探
究新知奠定良好的基础。】
二、 合作探究学习新知
148÷2
(一)动脑思考勇于探索
师:百位上的2变成了1, 想一想这会儿分小棒:会遇到什么
情况?
师:把一个百平均分成2份,每份分不到1个百,这样就不够分
了,不够分这可怎么办呢?
生1:拆开。(板贴:拆)
师:把一个百拆开,变成什么呢? (十个十)变成十个十就能分
了吗?拆开之后到底怎么分呢,让我们借助小棒一起动手分一分吧。
(二)合作探究展示交流
小组合作,教师巡视。
小组展示
1. 分3次。
生1:我们组是这样分的 ……
师:同学们看明白这位同学的分法了吗?我们一起来说一说这个
小组分的过程:
师:这样一共分了几次? (三次)先分了什么?再分什么?最后
分的……
2. 分两次。
生2:我们组是这样分的 ……
师:同学们,你们看明白了这个小组是怎样分的吗?
第一种分法分了3次,你们觉得哪种分法更好呢?为什么?
-----第二种更合理更简洁
师总结:因为10个十和4个十计数单位相同就可以合起来分一
次。 3. 回顾过程加深理解。
师:大家都比较认同这种分法是吗?那我们一起来回顾一下这种
分法。(课件演示)
(三)学习竖式理解算理。
1.独立尝试竖式。
师:同学们,你能把刚才分小棒的过程,用竖式表示出来吗?
(生尝试竖式计算)
2.梳理竖式的写法。
148÷ 2,先从被除数的最高位除起,先用百位上的1除以2,1 比2小,所以百位上不够除,不够除怎么办?不够除就和十位上的4 合起来,也就是看被除数的前两位,用14个十除以2,商7个十,
所以7写在商在哪个数位上? (十位)7为什么写在商的十位上?
总结:同学们,借助前面的动手操作,我们明白了计算的道理, 又通过尝试,我们学会了用竖式计算,非常了不起!那你能解决生活
中的实际问题吗?
【设计意图:算理是计算的依据,是算法的基础,而算法则是算 理的具体体现。本环节我抓住明理会法的思路,充分尊重学生的认知 规律和心理期待,放手让学生尝试完成,并通过“7为什么写在商的 十位上?”这一问题引领学生深层次思考,使学生充分理解“为什么 这样算”和“怎样计算”的问题,真正做到“授人以鱼不如授人以
渔”。】
三、 巩固探究拓展延伸
1. 借助情境图巩固练习。 (课件呈现情境图)
仔细观察你都发现了哪些数学信息?根据这些数学信息你又能
提出什么数学问题?
师:我们先来解决第一个(葡萄的)问题。你能列出算式吗?能
给大家说说为什么要用除法计算呢?
师:谁来试试第二个问题怎样列算式呢?--同意吗?为什么这个 问题也用除法计算呢?---小结:395千克大枣,每箱5千克,需要
多少个箱子?就是求395里面有几个5?
我们来算一算这两道题吧。女生做第一题,男生做第二个问题,
---交流 女生交流。 男生的课件演示。
【设计意图: 著名数学家华罗庚曾说过:人们对数学产生枯燥 乏味、神秘难懂的印象,原因之一便是脱离实际。所以,教师要善于 引导学生用数学的眼光观察生活,让学生发现生活中的数学,采集生 活教学实例,通过数学活动,促使他们自觉地将数学与生活联系起来, 萌发应用意识。本环节通过聚焦葡萄展区,让学生针对这一幅图画提
出问题,直接切入这节课需要解决的主要问题。】
2. 比较判定商的位数。
师:同学们一起来看大屏幕:仔细观察这4道题都是三位数除以 一位数,它们的商到底有什么不同呢?我们今天学习的就是三位数除
以一位数(商是两位数)的笔算除法,板书完整(商是两位数)
师:同学们,你们知道吗,今天我们学习的商是两位数的除法就 是借助商是三位数的方法而来的。像这样借助旧知识解决新问题是我
们数学学习中非常重要的一种方法,这种方法叫类推。
【设计意图:数学知识绝不是孤立的存在,在前后的学段中一定
有其发生、发展的过程,只有把握其前后发展的联系,研究整个知识 链的结构关系,我们才能更好地把握这一知识发展中每一阶段的教学 目标。本环节,我引领学生借助已有的知识经验,将新旧知识进行对 比,使学生充分感受新知识不过是旧知识类推而来,不但厘清了知识
体系,更化解了对学习新知识的畏难心理,从而真正爱上数学。】
请同学们想一想:三位数除以一位数什么时候商是三位数?什么
时候商是两位数? --- (同位讨论)
师:同学们善于观察、发现不同,这真是一个了不起的发现,快 一起来读一读这个发现吧,那你能根据刚才的发现,判断下面各题的
商是几位数,为什么? 理由呢?
3.拓展延伸。
师:真是聪明的孩子,那聪明的你们能不能发现小蘑菇可能是几
(1)如果536÷()的商是两位数,小蘑菇是一位数,藏在小蘑
菇身后的数字可能是几?最大是几?
(2)如果536÷()的商是三位数,藏在我小蘑菇身后的数字可能
是几?最小是几?
【设计意图:练习是对知识的巩固与再次梳理,也是对思维的训 练与提升。因为本节课的知识点相对比较简单,所以我除了训练学生 的计算能力,更重的的是加强思维训练,看看学生是否能举一反三,
学以致用,提高学生思考问题的灵活性和敏捷性。】
四、话说收获,总结提升
师:我们一起来回顾一下这节课的学习过程。我们先复习了三位 数除以一位数(商是三位数)的除法,运用类推的学习方法我们又学 习了三位数除以一位数(商是两位数)的笔算除法,然后把他们进行 对比,通过对比,我们发现了:百位够除的商是三位数,百位不够除
的商是两位数,这个发现可以帮助我们不用计算就能判断出商的位数。
同学们你能判断一下四位数4875÷3的商是几位数吗?为什么?这个 算式呢?课下,请同学们用今天学到的计算方法试着算一算这两道题。
好今天这节课就上到这,下课。
【设计意图: 一堂课的结尾犹如一曲乐章的尾声,会带来余音缭 绕、回味无穷之感。本环节,我利用“知识线”和“情感线”两条主 线对本节课进行了回顾。首先将学习数学方法化纳入到学生的认知结 构中,强调数学知识的整体性和结构性,感受到利用类推规律可以解
决很多问题;真正感受到“课已尽而意无穷”的效果。】
,