(bluehouse456 全文整理)
同学们,很高兴能和大家一起学数学。今天我们一起来学习人教版五年级上册第六单元多边形面积中三角形的面积第二课时。
在上一节课我们研究了三角形的面积,还记得三角形的面积计算公式是怎么推导的吗?我们把三角形转化成学过的图形,然后通过学过的图形面积来推导出三角形的面积,能具体说说推导的过程吗?我们把两个一样的三角形拼成一个平行四边形。
然后观察发现三角形的底和平行四边形的底相等。
三角形的高和平行四边形的高也相等。
所以三角形的面积就是平行四边形面积的一半,又因为平行四边形的面积等于底乘高,那么三角形的面积就等于底乘高除以二。
掌握了三角形的面积计算公式可以做什么呢?生活中许多物体的形状都是三角形的,我们学习了三角形的面积计算公式后,就能解决生活中与三角形面积有关的问题了。
那么今天这节课,我们就利用三角形的面积计算公式一起来解决问题。
这些是生活中常见的交通警示标识,看一看你都认识吗?
我觉得第二个标识应该是提醒驾驶员要减速慢行。
第三个是人行横道的标识,提醒司机要注意礼让行人。这些标识牌大小一样,表示的含义不同,第一个代表的是注意危险,提示驾驶员注意观察路况,谨慎驾驶,最后一个是向右急弯路的警示。认识了这些交通标识,接下来你还想知道什么呢?我想知道一个标识牌的面积是多少?
要想知道面积,就要先知道它的底和高分别是多少。
这一组道路交通警示标识的底是九分米,高是7.8分米。
现在请你计算出一块标识牌的面积大约是多少平方分米,把你解决问题的过程记录下来。
屏幕前的同学们,你们完成了吗?我们一起来看看小勇是怎么做的,60盆底是九分米。
高是7.8分米,三角形的面积等于底乘高除以二,用九乘7.8除以二等于35.11块标识牌的面积是35.1平方分米。
你们和小勇的答案一样吗?自己检查一下吧,现在道路交通警示标识的面积我们解决了,你们在生活中还见过哪些三角形呢?
我还看见过形状是三角形的绿地呢。
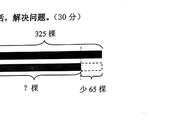
小雅真善于观察,发现了有的绿地的形状是三角形的。我们看公路中间有一块三角形空地,工人叔叔要在上面种上草坪美化环境。已知种一平方米草坪需要花20元,问种这片草坪需要花多少钱?除此之外,你还能从图中获取哪些信息?这块三角形空地的三条边分别是六米、八米和十米。
现在请你尝试解决问题,把过程记录下来。
屏幕前的同学们,你们都完成了吗?我们来交流一下,这是小林和小亮的做法,请你仔细观察他们的方法,说一说有什么发现。
我发现两位同学的思路一样,都是先计算出三角形空地的面积,然后用每平方米草坪的单价乘空地的面积,求出一共需要花多少钱。
但是他们计算出的三角形面积不一样,所以最后的价钱差了很多。
那他们谁做的对呢?
他们两个都选择了六米和八米作为三角形的底和高来计算面积,但是小亮在计算三角形面积的时候没有除以二,如果不除以二,求出的不是三角形的面积,而是和这个三角形等底等高的平行四边形的面积。
我明白了,我忘记除以二了,所以小明的答案是对的,我的是错的。我提醒大家,计算三角形的面积时,千万别忘记除以二。
对于这个问题还有什么其他的疑问吗?图中还告诉我们,三角形空地的斜边是十米呢,为什么没有用到十米这个数据呢?对呀,大家为什么都选择了六和八这两个数据,却没有选择十呢?
因为这是一个直角三角形,六米和八米是两条直角边的长度。
两条直角边就是一组对应的底和高,如果想用十米这个数据,就要先找到这条边对应的高才行,也就是需要从这条边所对的顶点向它做直线画出高测量以后再计算。
通过大家的讨论和分析,我们知道了在计算三角形面积的时候,也要找到对应的底和高,如果是一个直角三角形,选择两条直角边来计算比较方便。另外,在计算三角形面积的时候,千万要记得除以二。
接下来我们再帮小林检查一下,看看他第二步做对了吗?
通过检查验算,我们知道小林的解答是正确的,种这片草坪需要480元,你们看,这块空地也是三角形的,你能想办法求出它的面积吗?
这个空地的形状是钝角三角形,求面积也要找到对应的底和高。如果是你,你打算测量哪组底和高?我觉得测量最长的这条边,把它当做底,然后再找到它对应的高,从这条最长的边所对应的顶点向底边做垂线,就是最长边所对应的高。
如果用较短的一条边做底,怎么找到高呢?
钝角三角形较短的两条边所对应的高需要通过做短边的延长线才能找到。
我们一起来看一看。
用这条短边做底,因为这条边所对的顶点在这里,所以要先画出这条边的延长线,然后从这个顶点向延长线做垂线,从而找到这条短边所对应的高。我明白了钝角三角形短边对应的高在三角形外。
那我觉得还是用最长的边做底,这样高就在三角形内比较好找。
是的,其实每个三角形都有三组对应的底和高,但是我们在实际解决问题的时候,还是要找比较容易测量的底和高来进行计算,最终解决问题。
已知三角形的底和高求面积,同学们都掌握了,那换一个角度,已知一个三角形的面积和底求高,你们会吗?谁先来说一说,从题中你能获取哪些信息?
我知道了三角形的面积是176平方厘米,底是22厘米,需要我们求出三角形的高是多少厘米?
怎么样,有想法了吗?把你解决问题的过程记录下来。
这是小丽的做法,他做的对吗?
如果高14,带入的原体检查四乘22除以二等于44平方厘米,算出的面积是44平方厘米,和原题中给出的面积不相等。
那你们看一看,想一想,小丽错在哪里了?不应该用面积除以二,不应该用面积除以二,这是为什么呢?应该怎样做呢?
因为我们知道三角形的面积计算公式是底乘高除以二,那么面积是底乘高的积除以二的商,所以我们就逆着推,先用面积乘二求出底乘高的积,然后再逆着推,用求出的积除以底就等于高。所以列式应该是176乘二除以22,算出来高是16厘米。
这个结果对吗?我们也检验一下,如果高是16,用22乘16除以二等于176平方厘米和题目中的面积是一样的,说明结果正确。看来根据三角形面积计算公式逆着往回推,可以找到计算三角形高的方法,即面积乘二除以底等于高。还有其他方法吗?
我画图再给大家讲一讲为什么要先乘二。我先画了一个和原来的三角形一样的三角形,然后把这两个三角形拼成了一个平行四边形。
平行四边形的底与三角形的底相等,高就是三角形的高,所以相当于把问题转化成求平行四边形的高是多少厘米?已知一个三角形的面积是176平方厘米,所以平行四边形的面积就是176乘二等于352平方厘米。
又因为平行四边形面积公式时,S等于ah,所以用求出的面积352除以底长22算出的高也就是三角形的高。
小亮利用了转化的思想,把三角形转化成平行四边形,因为拼成的平行四边形和原来的三角形高相等,进而求出了三角形的高是16厘米。同学们不仅灵活的利用了三角形计算公式逆推出求高的方法,还运用转化的方法解释了这样做的道理。老师还发现有同学是这样解决问题的,我们一起看看小雅是怎么做的我十例方程解决问题的。
设三角形的高是X厘米,然后根据三角形面积的计算公式列出方程是22X除以二等于176。
再根据等式的性质解方程,最后求出X等于16,也就是三角形的高是16厘米。同学们太棒了,又联想到了上一单元我们学过的有关方程的知识,用列方程的方法解决了问题,那和前面的方法比一比,你们有什么感受吗?我发现用方程的方法不用逆着往回推,根据三角形面积的计算公式列出方程就可以了。
希望同学们也能够根据实际问题选择合适的方法解决问题。下面这个任务有一点挑战性,下图中哪几对三角形的面积是相等的?请你先观察图,看一看能获得哪些信息。我观察到三角形ABC和三角形DC。
有一条共用的边就是BC。
两条虚线互相平行,我们要找到图中面积相等的三角形。我记得我们在研究平行四边形时,曾经找过平行线间面积相等的平行四边形,我们发现了等底等高的平行四边形面积是相等的。
所以我就想知道,等底等高的三角形,面积是不是也相等呢?
那我们就带着小勇的猜想,想一想,画一画,找出图中面积相等的三角形开始吧。
屏幕前的同学们,你们完成了吗?我们交流一下。我先找到的面积相等的两个三角形分别是三角形ABC和三角形DC,因为这两个三角形的底相同,又因为平行线间的距离处处相等,所以这两个三角形的高也相等。
它们的面积都是用BC的长度乘平行线间的距离再除以二,那么它们的面积一定是相等的。
小丁找到的两个面积相等的三角形,你们同意吗?对于前面小勇的猜想,你们有什么想说的?
看来,不仅等底等高的平行四边形面积相等,等底等高的三角形面积也是相等的,所以刚才小勇的猜想是正确的。
还有其他的发现吗?图中还有没有面积相等的三角形?
我觉得三角形Abe和三角形DCE的面积也应该是相等的。
小兰说的这两个三角形你找到了吗?它们的面积相等吗?
我看不出这两个三角形是不是等底等高,没法比较。这两个三角形的面积是相等的,可以这样比,刚才已经知道三角形ABC和三角形BC面积相等。
这两个三角形有重叠的部分。
即三角形BCE。
用三角形ABC和三角形BCE同时减去三角形B,那剩下的部分三角形Abe和三角形BCE的面积自然也是相等的。
看着图想想小同的分析和比较的过程,你同意吗?我们在图中找到了面积相等的三角形,你还能画出和三角形ABC面积相等的三角形吗?试一试。
老师,这里收集了两位同学的作品,你们快看看他们画的对不对呢?
我觉得他们画的都是对的。
因为他们都是以BC作为三角形的底,以两条平行线间的距离为高。
画出的三角形,那么它们都和三角形ABC等底等高。
所以面积都和三角形ABC的面积相等。
老师相信你们也一定画出了和三角形ABC面积相等的三角形,在这组平行线间,你能画出多少个和三角形ABC面积相等的三角形?
能画无数个,只要保证和三角形ABC等比等高,那它们的面积就都是相等的。
同学们,通过这节课的学习,你们都有哪些收获?我能灵活的利用三角形面积公式解决问题。我还想提醒大家,计算三角形面积时别忘了除以二。
我知道了,等底等高的三角形形状可能不同,但是面积一定相等。
我发现转化的方法不仅能帮助我们推导公式,在解决问题中也会用到转化的方法。通过这节课的学习,同学们不仅能利用三角形的面积计算公式解决生活中的实际问题,还对三角形的底高和面积之间的关系有了更深入的理解。
今天我们学习的具体内容在数学书第91至92页,大家课后可以自主复习。课后练习一、完成数学书第91页第二题,二、完成数学书第91页第五题。同学们,这节课我们就上到这里。
,