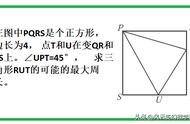
本题求三角形周长的最小值,利用的为将军饮马模型,这也是周长最小值中比较简单的一种类型。

2.相似三角形(转化法)
例题2:如图,在平面直角坐标系中,点A,B的坐标分别为(-4,0),(2,0),点C在y轴上,其坐标为(0,-3),抛物线经过点A,B,C.P为第三象限内抛物线上一动点.
(1)求该抛物线的解析式.
(2)连接AC,过点P作PD⊥AC,PE∥y轴交AC于点E,当△PDE的周长最大时,求P点的坐标和△PDE周长的最大值.

分析:(1)由点A,B的坐标可设抛物线的交点式,再将点C代入即可。

先证△PDE∽△AOC,推出△PDE的周长=PD PE DE=12/5PE,三角形的周长最值转化为线段最值,求出直线AC的解析式,利用设点法,表示出线段PE的长度,求出PE的最大值,即可写出点P坐标及△PDE周长的最大值。