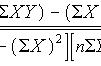通常指Pearson product-moment correlation coefficient,统计学参数,用来研究变量间的相关性,通常描述变量间的线性相关性。其范围介于-1和1之间,其绝对值越接近1,说明变量间的相关性越大。
- 当r>0的时候,我们认为两个变量之间是正相关的;
- 当r<0时,两个变量之间是负相关的。当r=0时,两个变量之间是线性无关的。
- 当r=-1和1时,两个变量之间的相关性可以用一次函数(直线的形式)来描述。

相关系数r的范围
Pearson相关系数的计算公式如下:

Pearson相关系数计算公式
该公式将变量x和y的协方差与变量x和y的方差积的根号值的比值作为新的参数来衡量变量x和y之间相关性。Pearson相关系数的好处在于归一化了系数的范围,不用考虑量纲值对参数评价的影响,但是该系数有一定的局限性,并不能完全描述所有变量的相关性。除此之外描述变量相关性的系数还有Spearman correlation coefficient(斯皮尔曼相关性系数)和Kendall(肯德尔相关性系数)系数。Spearman系数用于描述具有顺序属性的变量序列,而Kendall序列用于描述具有类别属性的变量。
如何计算Pearson等相关系数呢?明确了这些系数之后,重点在于如何计算这些系数。可以通过一些统计分析软件,去计算这些系数,常用的有Origin和Spss等。此外也可以使用python和Matlab的库函数很容易求得这些变量之间的相关系数。以Origin为例:

我们首先可以导入需要分析的变量值到一个工作簿中,然后进入Origin统计菜单,然后点击相关系数进入相关系数页面