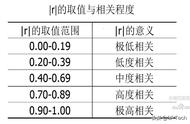
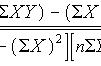假设有一个虚拟的数据集包含多对变量,即每位母亲和她女儿的身高:

通过这个数据集,我们如何预测另一位身高为63的母亲的女儿的身高?
方法是用线性回归。
首先找到最佳拟合线,然后用这条直线做预测。

线性回归是寻找数据集的最佳拟合线,这条线可以用来做预测。
如何找到最佳拟合线?
这就是为什么我们需要使用梯度下降。
梯度下降是一种找到最佳拟合线的工具。
在深入研究梯度下降之前,先看看另一种计算最佳拟合线的方法。
最佳拟合线的统计计算方法:
直线可以用公式表示:y=mx b。
回归线斜率m的公式为:m = r * (SD of y / SD of x)。
转换:x和y值之间的相关系数(r),乘以y值的标准差(SD of y)除以x值的标准偏差(SD of x)。
以上数据中母亲身高的标准差约为4.07,女儿身高的标准偏差约为5.5,这两组变量之间的相关系数约为0.89。
因此,最佳拟合线或回归线为:
y = 0.89*(5.5 / 4.07)x b
y = 1.2x b
我们知道回归线穿过了平均点,所以线上的一个点是(x值的平均值,y值的平均值),其中有(63.5,63.33)。
63.33 = 1.2*63.5 b
b = -12.87
因此,使用相关系数和标准差计算的回归线近似为:
y = 1.2x - 12.87
使用统计学的回归线为y=1.2x-12.87。
接下来让我们研究梯度下降。
计算最佳拟合线的梯度下降法:
在使用梯度下降法时,我们从一条随机线开始,一点一点地改变直线的参数(即斜率和y轴截距),以得到最佳拟合的直线。
那么我们怎么知道什么时候到达最合适的位置呢?
对于尝试的每一条直线——直线A、直线B、直线C等等——我们都要计算误差的平方和。比如:如果直线B的值比直线A的误差小,那么直线B更适合,等等。